10.3.2 Instantaneous Free Acceleration

To find the free acceleration of an underconstrained mechanism a FreeSystem object is built that contains a new set of equations of motion with one or more constraints dropped from the model.

Instantaneous free acceleration.

The two RelativeAngle1 constraints are now dropped from the robot arm to give the model two degrees of freedom. If initial conditions are not specified, SetFree takes them from the current default initial guesses LastSolve[].

This drops the constraints that lock the rotation of the joints.

In[10]:=

This solves the FreeSystem object.

In[11]:=

Here is the resultant acceleration vector at the tip of link 2.

In[12]:=

Out[12]=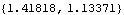

To find the free acceleration corresponding to a sequence of different values of loadangle, SetParameters could be used between each successive run of SolveFree, or the InitialCondition option can be used to pass SolveFree the new parameter values. SolveFree reads all its initial conditions from the InitialCondition option, Parameters[], and the initial conditions contained in the FreeSystem object, in that order.

This solves the FreeSystem object at 21 different values of loadangle.

In[13]:=

Here is a parametric plot of the X and Y components of the resulting acceleration at the tip of link 2. The diagonal line across the plot crosses the ellipse at loadangle = 0.

In[14]:=

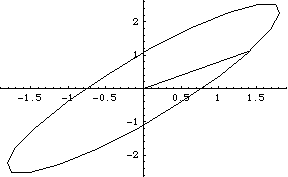
Out[14]=