4.1.4 3D Euler and Angular FormulationsVelocity and acceleration solutions are calculated in a 3D model in the same manner as in a 2D model. However, there are three options in a 3D model as to how the higher-order data is represented.
Since the angular orientation of Modeler3D bodies is specified by four Euler generalized parameters, {Eon, Ein, Ejn, Ekn}, one way of representing the angular velocity and acceleration of a body in 3-space is with the first and second derivatives of the Euler parameters, {Eond, ...} and {Eondd, ...}. Another more familiar way of representing angular velocity and acceleration is with the angular velocity and acceleration vectors, {omegaX, omegaY, omegaZ} and {alphaX, alphaY, alphaZ}, in either global coordinates or local coordinates attached to each individual body. Modeler3D can formulate the higher-order solutions in any of these representations, each of which requires that different sets of equations be built by the SetConstraints function. Which formulation is used is specified with the Method and Coordinates options for SetSymbols.

A system set-up function. The Method option for SetSymbols may also be used with Modeler2D to specify angular coordinates or a degenerate version of Euler coordinates, although the Euler coordinates are seldom used in 2D models. Specifying Method -> Euler in a Modeler2D model causes the angular orientation of each body to be represented by a pair of coordinates {Ejn, Ekn} = {cos( n), sin( n), sin( n)} instead of a single coordinate, n)} instead of a single coordinate,  n. Velocity and acceleration are also represented by the coordinate pairs {Ejnd, Eknd} and {Ejndd, Ekndd}. The inclusion of this feature in Modeler2D is largely academic; specifying Method -> Euler causes four equations to be generated for each body, instead of only three, and usually slows down the solution phase. There are two advantages afforded by 2D degenerate Euler coordinates: no trigonometric functions are generated in the constraint expressions so all of the constraints are purely algebraic, and the second derivative of a 2D rotation matrix is very simple which leads to faster solutions in some dynamical systems. n. Velocity and acceleration are also represented by the coordinate pairs {Ejnd, Eknd} and {Ejndd, Ekndd}. The inclusion of this feature in Modeler2D is largely academic; specifying Method -> Euler causes four equations to be generated for each body, instead of only three, and usually slows down the solution phase. There are two advantages afforded by 2D degenerate Euler coordinates: no trigonometric functions are generated in the constraint expressions so all of the constraints are purely algebraic, and the second derivative of a 2D rotation matrix is very simple which leads to faster solutions in some dynamical systems. 2D/3DAn option for SetSymbols. 3DAn option for SetSymbols. The MacPherson strut front model defined in Section 4.1.3 is used to demonstrate the 3D velocity and acceleration solutions. The Solution -> Velocity option causes SolveMech to calculate the location and velocity of each body in the model. This finds the location and velocity of each body at T = 2.5.
Out[45]= | 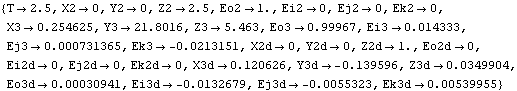 |
Note that the angular velocity of each body is returned in the form of derivatives of Euler parameters. This is because the constraint equations were built with all default options for SetSymbols. If the model is rebuilt with the Method -> Angular option for SetSymbols, the first derivatives of the Euler parameters will be replaced by angular velocities. This rebuilds the constraints with angular velocity formulation. Now find the velocity solution at T = 2.0.
Out[48]= |  |
The angular velocity of the chassis in global coordinates is represented by the symbols {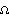 x2, x2, 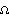 y2, y2, 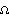 z2}. z2}.
The Solution -> Acceleration option causes SolveMech to calculate the location, velocity, and acceleration of each body in the model. Note that it takes more time to execute the following command the first time than it will on all subsequent executions. This is because the acceleration equations must be built the first time through. Now find the acceleration of the bodies at T = 2.0.
Out[49]= |  |
Since angular acceleration is the first derivative of angular velocity, the angular acceleration vector of the carrier, is represented by the derivatives of the angular velocity {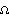 x3d, x3d, 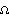 y3d, y3d, 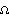 z3d}. z3d}.
The model is now rebuilt with the Coordinates -> Local option so that angular velocity is represented in local, instead of global, coordinates. This rebuilds the constraints with a local angular velocity formulation. Now find the velocity solution at T = 2.0.
Out[52]= |  |
Note that the local angular velocity of body 3 is only slightly different from the global angular velocity. This is because the angular orientation of the wheel carrier is very close to being aligned with the global coordinate system.
|