Plots of the characteristic values, or the characteristic loci, for a system can be determined by using the function CharacteristicValuePlot. | CharacteristicValuePlot[system] |
| | plot the behavior of the characteristic values of the object system |
| CharacteristicValuePlot[system, {w, wmin, wmax}] |
|
| | plot the behavior of the characteristic values for frequency w running from wmin to wmax |
Creating the characteristic value plot. Make sure the application is loaded. This is the transfer-function matrix model of a two-input, two-output system, with one unstable pole at s=+3. | Out[3]= | 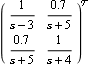 |
These are the characteristic value plots of this system. 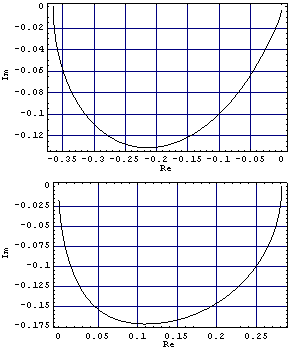
The first plot starts at about {-0.365, 0} at a low frequency close to zero, and approaches the origin in a counterclockwise direction at the higher frequencies. The second plot starts at about {0.28, 0} at a low frequency close to zero, and approaches the origin in an clockwise direction at the higher frequencies. The generalized Nyquist stability theorem requires a net sum of encirclements of the critical point {-1, 0} by the characteristic values equal to the number of unstable poles of the open-loop system. As neither of the characteristic value plots encircles its critical point at {-1, 0}, the closed-loop system with unity negative feedback will be unstable. You can confirm this, by determining the poles of the resulting closed-loop system. This determines the closed-loop system with unity negative feedback. | Out[6]= | 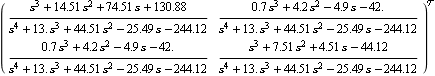 |
As expected, one closed-loop pole has a positive real part. | Out[8]= | 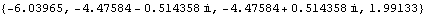 |
Here is a forward-path compensator that applies equal gains of 5 to each system input. | Out[10]= | 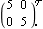 |
This determines the resulting forward-path transfer-function matrix for the system, with this compensator applied. | Out[12]= | 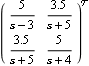 |
The characteristic value plots of the forward-path transfer-function matrix of this system now exhibit one net counterclockwise encirclement of the critical point {-1, 0}, and the closed-loop system with unity negative feedback will be stable. 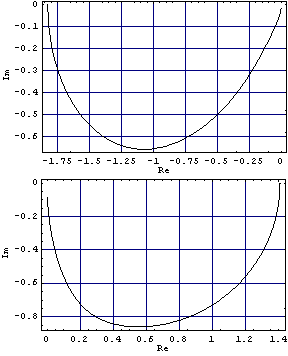
This determines the transfer-function matrix of the resulting closed-loop system, with unity negative feedback. | Out[15]= | 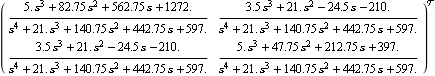 |
As expected, the closed-loop system is now stable. | Out[17]= | 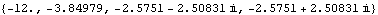 |
|