Sometimes, you may wish to determine rational function approximations to the elements of the Perron-Frobenius eigenvector using an alternative fitting method, or you may want to explore the possibility of further simplifying the compensators obtained with the previous semi-automatic procedure, and may be prepared to accept a slightly less optimal solution. You can do this by creating your own dynamic scaling compensator. Make sure the application is loaded. This is the two-input, two-output transfer-function object, considered earlier in Section 5.3.1. | Out[3]= | 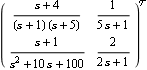 |
This generates the behavior of the elements of the Perron-Frobenius right eigenvector with element 2 normalized, as a function of frequency. 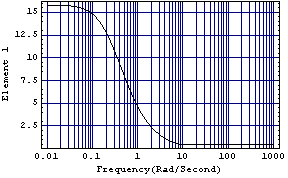
After some trial and error, you might arrive at the following rational function, as a good approximation to the behavior of element 1 of the Perron-Frobenius eigenvector. | Out[6]= | 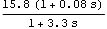 |
This sets up a dynamic input-scaling compensator for the system, using this function. | Out[8]= | 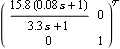 |
This is the amplitude behavior of this compensator with frequency. 
The compensator gives a good approximation to the eigenvector element. 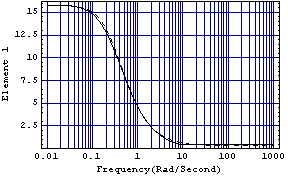
This applies the compensator to the system. This scales up row 2 of the Nyquist array. Here is the resulting Nyquist array, which is clearly diagonal dominant. 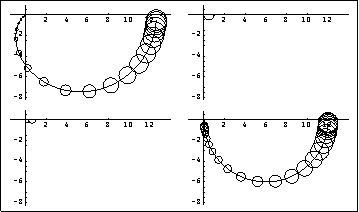
|