WOLFRAM

Legacy Documentation

Polynomial Control Systems (2014)

This is documentation for an obsolete product.
Current products and services

Function Index / Linear System Analysis /
Previous section-----Next section

4.4.1 Detecting Input and Output Decoupling Zeros

The functions InputDecouplingZeros and OutputDecouplingZeros can be used to determine any input or output decoupling zeros present in a system matrix model in polynomial, or state-space, form.

InputDecouplingZeros[system]
return a list of any input decoupling zeros in the system matrix object system
OutputDecouplingZeros[system]
return a list of any output decoupling zeros in the system matrix object system

The InputDecouplingZeros and OutputDecouplingZeros functions.

Make sure the application is loaded.

In[1]:=

Here are some polynomial matrices.

In[2]:=
In[3]:=
In[4]:=

This is the corresponding system matrix.

In[5]:=
O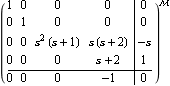ut[6]=

You can check if the matrices T(s) and U(s) are coprime by using the function LeftCoprime.

In[7]:=
O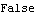ut[8]=

Since T(s) and U(s) are not left coprime, you can determine the left matrix GCD L(s) by using the function LeftGCDDecomposition, and hence determine the input decoupling zeros as the roots of the determinant of L(s).

In[9]:=
In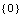[10]:=
Out[11]=

The same result can be obtained more directly by applying the function InputDecouplingZeros to the SystemMatrix object.

In[12]:=
O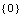ut[13]=

You can also check if the matrices T(s) and V(s) of the SystemMatrix object are coprime by using the function RightCoprime.

In[14]:=
O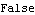ut[15]=

Since the matrices T(s) and V(s) are not right coprime, the output decoupling zeros of this system can be determined by using the function OutputDecouplingZeros.

In[16]:=
O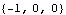ut[17]=

Equally, you can determine the output decoupling zeros of the system matrix object, after the input decoupling zero has been removed, by applying the function OutputDecouplingZeros to the system matrix consisting of the polynomial matrices Tr, Ur, V, and W.

Here is the system matrix object after the input decoupling zero has been removed.

In[18]:=
O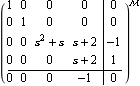ut[19]=

You can obtain the same result using the function RemoveInputDecouplingZeros, introduced later in Section 4.4.2.

In[20]:=
O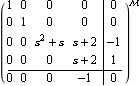ut[21]=

The matrices Tr and V of this system matrix are not right coprime.

In[22]:=
O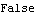ut[23]=

Hence, this system has output decoupling zeros.

In[24]:=
O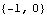ut[25]=

Here is a state-space system.

In[26]:=
O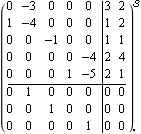ut[27]=

You can test if this state-space system is controllable by using the function Controllable.

In[28]:=
O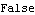ut[29]=

Here is the system matrix, in the variable s, corresponding to the state-space object ss.

In[30]:=
O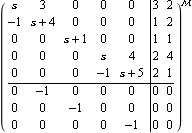ut[31]=

This confirms that the underlying state-space model is uncontrollable, and gives the decoupling zero.

In[32]:=
O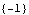ut[33]=

The function OutputDecouplingZeros is used in an analogous manner.