The transmission zeros of a system are all zeros of polynomials  i(s) (see Eq. (4.7)) in the numerator terms of the McMillan form of the TransferFunction object. These are the values of s for which the transfer-function matrix loses rank. They are also the locations in the s-plane to which the multivariable system poles tend under infinite feedback gains, in a root-locus sense.
For the system considered earlier in Example 4.1, the transfer-function model i(s) (see Eq. (4.7)) in the numerator terms of the McMillan form of the TransferFunction object. These are the values of s for which the transfer-function matrix loses rank. They are also the locations in the s-plane to which the multivariable system poles tend under infinite feedback gains, in a root-locus sense.
For the system considered earlier in Example 4.1, the transfer-function model was shown to have the McMillan form from which it can be seen that this system has one transmission zero at s = +1. This means that two of the system poles will be attracted into the right half-plane, with one approaching this zero, and the other tending to +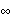 , under feedback gain.
Once a zero appears in one of the numerator terms of the McMillan form of a system, it will also appear in all subsequent numerator terms of the McMillan form. In this example, this tells the designer that after the first feedback loop is closed with a high gain, a right half-plane zero at s = +1 will appear in the second loop, and all subsequent loops.
The transmission zeros can be determined, for all the model forms now implemented, by using the function TransmissionZeros. , under feedback gain.
Once a zero appears in one of the numerator terms of the McMillan form of a system, it will also appear in all subsequent numerator terms of the McMillan form. In this example, this tells the designer that after the first feedback loop is closed with a high gain, a right half-plane zero at s = +1 will appear in the second loop, and all subsequent loops.
The transmission zeros can be determined, for all the model forms now implemented, by using the function TransmissionZeros. | TransmissionZeros[system] | return a list of the transmission zeros of the object system | | TransmissionZeros[m, var] | return a list of the transmission zeros of the rational polynomial matrix m in the variable var |
The TransmissionZeros function. Make sure the application is loaded. Here is a two-input, two-output transfer function. | Out[3]= | 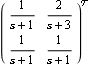 |
This is a list of its transmission zeros. | Out[5]= | 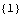 |
You can also apply the function TransmissionZeros directly to a rational polynomial matrix. | Out[7]= | 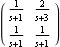 |
| Out[9]= | 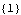 |
Due to this right half-plane transmission zero, it is not possible to set up two simultaneous feedback loops with a gain > 10, say, around this apparently simple multivariable system, and maintain stability. Here is simple forward-path compensator with two gains = 100. | Out[11]= | 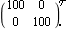 |
Here is the resulting closed-loop system with unity feedback. | Out[13]= | 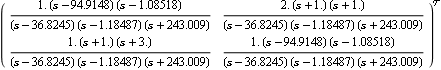 |
Here is its McMillan form. | Out[15]= | 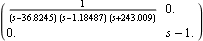 |
As the system transmission zeros do not change under constant output feedback, the transmission zero at s = +1 remains unchanged by this feedback, but two of the system poles have been attracted into the right half of the s-plane, and one is approaching the transmission zero at +1, namely, the pole at s = 1.18487, and the other is going toward +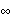 ; namely, the pole at s = 36.8245. ; namely, the pole at s = 36.8245. |