The transformation to Luenberger observable canonical form, introduced here, is used in the design of the Luenberger reduced-order state-estimator discussed in Section 6.5. Given an n"th"-order linear system in state-space form, as described by Eq. (6.7), then using a transformation matrix T formed from the rows of the observability matrix for the pair {A, C}, the resulting matrices 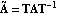 and and 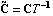 have special block structured forms, namely, for a system with q outputs, have special block structured forms, namely, for a system with q outputs, where the diagonal blocks 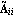 are in the observable companion form are in the observable companion form for i = 1, ..., q, with dimensions  i× i× i, and the symbol * stands for possible nonzero entries. The off-diagonal blocks i, and the symbol * stands for possible nonzero entries. The off-diagonal blocks 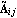 have zero entries, except perhaps in the last column, that is, these look like the have zero entries, except perhaps in the last column, that is, these look like the 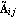 of the Luenberger controllable canonical form (see Section 6.4.1) transposed.
The transformed output matrix of the Luenberger controllable canonical form (see Section 6.4.1) transposed.
The transformed output matrix 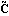 is is where the q × i blocks i blocks 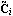 have the special form have the special form and the unit entry in the first row occurs in the last column. The entries below the unit entry in the last column of 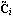 are not, in general, equal to zero. These nonzero entries in the matrix are not, in general, equal to zero. These nonzero entries in the matrix 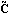 can be readily removed, if desired, by a simple nonsingular transformation of the system outputs. can be readily removed, if desired, by a simple nonsingular transformation of the system outputs. Here, the matrix 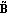 has no special form. has no special form. The parameters  k that appear in the formulation are the observability indices of the system, and are determined in a similar way to the controllability indices, defined in Section 6.4.1, but using the rows of the observability matrix for the system. The observability index for the system is defined as k that appear in the formulation are the observability indices of the system, and are determined in a similar way to the controllability indices, defined in Section 6.4.1, but using the rows of the observability matrix for the system. The observability index for the system is defined as  o= Max[ o= Max[ i]. The function ObservabilityIndices can be used to determine these. i]. The function ObservabilityIndices can be used to determine these. | ObservabilityIndices[statespace] |
| | determine the observability indices of the system statespace |
Observability indices. The observable canonical form of the system and the required transformation matrix T are both generated via elementary row and column operations on the original system A and C matrices, using a version of Daly's algorithm (Daly (1976)). If a state-space system is completely observable, and the rows of its matrix C are linearly independent, then the function LuenbergerObservableForm can be used to transform the system into this canonical form. | LuenbergerObservableForm[statespace] |
| | find the Luenberger observable form of the system statespace |
Luenberger observable canonical form. Make sure the application is loaded. Consider a 5th-order state-space system with two inputs and two outputs. | Out[3]= | 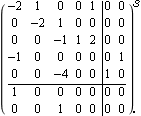 |
These are its observability indices. | Out[5]= | 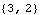 |
These indices indicate that in the corresponding Luenberger observable canonical form, the transformed matrix A will have two observable companion form diagonal blocks of size 3 × 3 and 2 × 2, with a two-block structured transformed matrix C. | Out[7]= |  |
The Control System Professional functions TransformationMatrix and SimilarityTransform are both applicable to the LuenbergerObservableForm. This gives the transformation matrix between the two realizations. | Out[9]= | 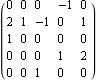 |
You can confirm the similarity transformation of the original system with this matrix. | Out[11]= |  |
|