The coprimeness tests illustrated in Example 4.3 can be carried out automatically by using the functions LeftCoprime and RightCoprime. | LeftCoprime[system] | test if the matrices d and n in the left matrix-fraction system are relatively left prime | | LeftCoprime[m{1}, m2, var]
RightCoprime[system]
RightCoprime[m{1}, m2, var] | test if the two polynomial matrices m{1} and m{2}, in the variable var, are relatively left prime
test if the matrices n and d in the right matrix-fraction system are relatively right prime
test if the two polynomial matrices m{1} and m{2}, in the variable var, are relatively right prime |
Testing the coprimeness. Make sure the application is loaded. Here are the matrices N(s) and D(s) of a right matrix-fraction model of a system. | Out[3]= |  |
| Out[5]= | 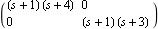 |
This constructs a block matrix  . . | Out[7]= |  |
This is its Smith form. | Out[9]= |  |
Since the leading 2 × 2 block of the Smith form is equal to the identity matrix I2, the two polynomial matrices describing the right matrix-fraction model are relatively right prime, or coprime, and hence no lower-order version exists that would create the same transfer-function matrix. Here is the same result obtained at once using the function RightCoprime. | Out[11]= |  |
Here is the corresponding right matrix-fraction object. | Out[13]= |  |
You can also apply the function RightCoprime directly to the matrix-fraction object. | Out[15]= |  |
Here is a LeftMatrixFraction object. | Out[17]= | 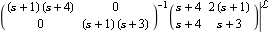 |
You can equally apply the function LeftCoprime directly to the matrix-fraction object. | Out[19]= |  |
|