A system is controllable (f), or functionally controllable, if given any suitable vector y of output functions defined for t > 0, there exists a vector u of inputs defined for t > 0, which generates the output vector y from the initial conditions x(0) = 0 (Rosenbrock (1970), and Patel and Munro (1982)). A suitable vector y is defined here as one that is sufficiently smooth to be generated without impulse functions in u, and which has a Laplace transform.
In terms of a system description given by Eq. (4.2) and Eq. (4.3), a system having q = p is functionally controllable if and only if its transfer-function matrix G(s) is nonsingular, that is, 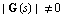 This is therefore a necessary requirement for regulator design, or servo-tracking system design.
If q > p, that is, if there are more outputs than inputs, then the system so defined is not functionally controllable.
If q < p, that is, if there are more inputs than outputs, then the system so defined is functionally controllable if and only if there exists at least one q × q nonzero minor of G(s).
The functional controllability of a system does not imply state controllability, and vice versa. Also, systems that have more outputs than inputs, and are therefore not functionally controllable, may be output controllable (see Section 7.1 of Control System Professional) since it may still be possible to drive the output vector to the origin in finite time. Consider a system described by the transfer-function matrix then Thus, the system is controllable (f). However, the fourth-order state-space realization which gives rise to G(s) in Eq. (4.14) is not state controllable.
Similarly, a system is controllable (l), or left half-plane controllable, if it is functionally controllable and all the zeros of the numerator polynomials in the McMillan form of G(s), that is the transmission zeros, lie in the open left half of the complex-plane (Rosenbrock (1970)).
For the system of Eq. (4.14), the McMillan form of G(s) is So, although G(s) is controllable (f), it is not controllable (l). This tells the designer that it will not be possible to simultaneously set up two high-gain feedback loops around this system. |