WSMLink`
WSMLink`

WSMFindEquilibrium

WSMFindEquilibrium is being phased out in favor of FindSystemModelEquilibrium, which was introduced experimentally in Version 11.3.

WSMFindEquilibrium["mmodel"]

searches for an equilibrium to the model "mmodel".

WSMFindEquilibrium["mmodel",{{{x1,x10},…},{{u1,u10},…},{{y1,y10},…}}]

searches for an equilibrium, starting from the point xi=xi0, ui=ui0, and yi=yi0.

WSMFindEquilibrium["mmodel",{x1v1,…},…]

searches for an equilibrium, with variable xi constrained to have the value vi etc.

Details and Options

  • WSMFindEquilibrium returns a list {{{x1,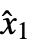},…},{{u1,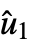},…},{{y1,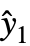},…}}, where 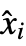, , 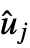and 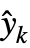are the computed equilibrium values for states, inputs, and outputs.
  • With no explicit starting point given, WSMModelData["mmodel","GroupedInitialValues"] is used.
  • An equilibrium for a differential algebraic system 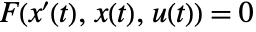is a value 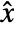and 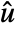such that .
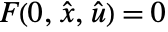  • WSMFindEquilibrium will attempt to find a local equilibrium point. In general, many equilibrium points may exist for a system.
  • The shortest unique model name mmodel can be used where WSMNames["*.mmodel"] gives a unique match.
  • The following options can be given:
  • WSMProgressMonitorAutomaticcontrol display of progress

Examples

open allclose all

Basic Examples  (4)

Load Wolfram System Modeler Link:

Find an equilibrium, starting the search at initial values:

Use given start values for states:

Use the diagram representation of a model as input:

Copy and paste the output above:

Scope  (3)

Give start values for states, inputs, and outputs:

Use constraints on inputs and outputs, and start values for states:

Find an equilibrium point with given constraints:

Applications  (5)

Find an equilibrium point for a single water tank with inflow and outflow:

Linearize a model around an equilibrium point:

Linearize around an equilibrium point and analyze the stability:

Design a PI controller for keeping the level in a tank with inflow and outflow constant:

Find the equilibrium where the level "h" is constrained to be 2:

Linearize and close the loop around a PI controller:

Show the closed-loop step response for a family of PI controllers:

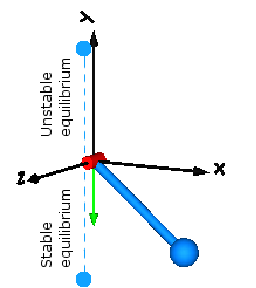
Simple pendulum swinging through any angle:

Equilibrium with the pendulum hanging straight down:

Pendulum standing straight up above its axis:

Level curves of the first integral give the potential energy of the system:

The pendulum has one stable and two unstable equilibrium points:

Properties & Relations  (2)

Equilibrium points , for an ODE satisfy :

Find an equilibrium point and :

Verify :

Many equilibrium points may exist: