WSMLink`
WSMLink`
WSMLinearize
WSMLinearizeは,バージョン11.3で試験的に導入されたSystemModelLinearizeに段階的に置き換えられつつある.
WSMLinearize["mmodel"]
平衡でモデル "mmodel" に線形化された状態空間を与える.
WSMLinearize["mmodel",{{{x1,x10},…},{{u1,u10},…}}]
状態値{x10,…}と初期値{u10,…}で線形化する.
詳細とオプション
- WSMLinearizeは,Wolfram SystemModelerで設計された連続時間系を線形化する.
- WSMLinearizeはStateSpaceModelオブジェクトを返す.
- WSMLinearize["mmodel",spec]は,spec に以下の記号的な値を許す.
-
"EquilibriumValues" WSMFindEquilibrium["mmodel"]を使う "InitialValues" WSMModelData["mmodel","GroupedInitialValues"]を使う - WSMLinearize["mmodel",vals,spec]は spec を使って,vals の欠落値を加える.
- デフォルトの spec は,"EquilibriumValues"であるとみなされる.
- 結果のStateSpaceModelは"mmodel"で定義されるように,状態 xi,入力 uj,出力 yk を持つ.
- 状態,入力,出力のリストは,WSMModelData["mmodel",spec]から求めることができる.
-
"StateVariables" 状態変数 xi "InputVariables" 入力変数 uj "OutputVariables" 出力変数 yk - WSMLinearizeは,微分代数方程式系を常微分方程式系に簡約し,結果の常微分方程式を線形化する.
- 状態方程式
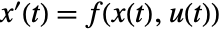 と出力方程式
と出力方程式 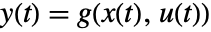 を持つ常微分方程式系は,点
を持つ常微分方程式系は,点 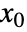 および
および 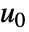 で線形化される.
で線形化される. - 線形化された系は,状態
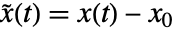 ,入力
,入力 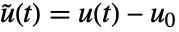 ,出力
,出力 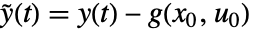 を,状態方程式
を,状態方程式 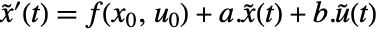 および出力方程式
および出力方程式 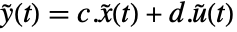 で持つ.行列は,
で持つ.行列は,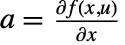 ,
,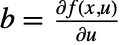 ,
,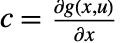 ,
,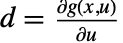 で与えられる.これらはすべて
で与えられる.これらはすべて 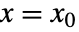 および
および 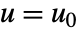 で評価される.
で評価される. - 返されたStateSpaceModelは,系
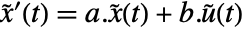 ,
,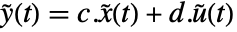 に相当する.
に相当する. - WSMNames["*.mmodel"]が一意的なマッチを与えるところでは,最短の一意的なモデル名 mmodel を使うことができる.
- 与えられるオプション:
-
Method "NumericDerivative" 線形化アルゴリズム用のメソッド WSMProgressMonitor Automatic 進捗の表示を制御する - オプションMethodが取り得る設定:
-
"NumericDerivative" SystemModelerの線形化を使う "SymbolicDerivative" StateSpaceModelの線形化を使う
例題
すべて開くすべて閉じる例 (4)
スコープ (13)
一般化と拡張 (1)
結果のStateSpaceModelでラベルを隠す:
オプション (4)
Method (4)
デフォルトで"NumericDerivative"メソッドが使われる:
メソッド"SymbolicDerivative"は,StateSpaceModelを使って系の方程式を線形化する:
アプリケーション (9)
線形化系の解析 (5)
シミュレーションのデータ上のFourierを使って結果を確かめる:
特性と関係 (8)
WSMModelDataを使って初期値付近で線形化する:
WSMFindEquilibriumを使って平衡付近で線形化する:
TransferFunctionModelを使って,伝達関数表現に変換する:
ToDiscreteTimeModelを使って,線形化されたモデルを離散化する:
StateSpaceModelは,常微分方程式の系を線形化することができる:

