ARCHProcess
ARCHProcess[κ,{α1,…,αq}]
表示通过标准白噪声驱动的 q 阶自回归条件异方差过程.
ARCHProcess[κ,{α1,…,αq},init]
表示初始数据为 init 的 ARCH 过程.
更多信息

- ARCHProcess 是一个离散时间和连续状态的随机过程.
- 如果条件均值 Expectation[x[t] {x[t-1], …}]=0 且由 Expectation [x[t]2{x[t-1, …}] 给出的条件方差
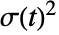 满足方程
满足方程 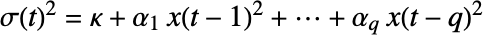 ,则 x[t] 为 ARCH 过程.
,则 x[t] 为 ARCH 过程. - 初始数据 init 可以用列表
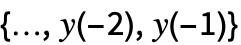 或时间标记为
或时间标记为 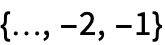 的单一路径 TemporalData 对象的形式给出.
的单一路径 TemporalData 对象的形式给出. - 标量 ARCH 过程可具有非负系数 αi 和正系数 κ.
- ARCHProcess[q] 表示阶数为 q 的 ARCH 过程,以用于 EstimatedProcess 及相关函数.
- ARCHProcess 可以与诸如 RandomFunction、CovarianceFunction 和 TimeSeriesForecast 等函数结合使用.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (13)
基本用法 (8)
一个集成的 ARCHProcess:
一个发散的 ARCHProcess:
ARCHProcess 成为协方差平稳过程的条件:
ARCHProcess[2] 具有二阶平稳性的区域::
估计 ARCHProcess:
过程切片性质 (5)
属性和关系 (3)
ARCHProcess 的值是互不相关的:
对应的 ARProcess:
ARCHProcess 的平方值服从 ARProcess:
Wolfram Research (2014),ARCHProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ARCHProcess.html.
文本
Wolfram Research (2014),ARCHProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ARCHProcess.html.
CMS
Wolfram 语言. 2014. "ARCHProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ARCHProcess.html.
APA
Wolfram 语言. (2014). ARCHProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ARCHProcess.html 年