CauchyMatrix

CauchyMatrix[x,y]

生成ベクトル x および y を構造化配列とすることで得られたコーシー(Cauchy)行列を表す．

CauchyMatrix[x]

CauchyMatrix[x,x]に等しい．

CauchyMatrix[cmat]

コーシー行列 cmat を構造化配列に変換する．

詳細とオプション

  • コーシー行列は，構造化行列として表されている場合はより効率的格納が可能で，Det，Inverse，LinearSolve等のより効率的な操作ができる．
  • コーシー行列は特異カーネルによる積分方程式の有理補間，等角写像，n-体シミュレーション，離散化等に関連した計算に出現する．
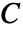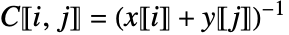  • 生成ベクトルの x と y が与えられた場合，結果のコーシー行列 は で与えられる成分を持つ．
  • 次は，CauchyMatrixによって加速される操作である．
  • Dettime
    Inversetime
    LinearSolvetime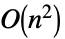
  • CauchyMatrix sa についての以下の特性"prop"には sa["prop"]でアクセスできる．
  • "XVector"生成ベクトル x
    "YVector"生成ベクトル y
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列によって保存されている内部データ
    "StructuredAlgorithms"構造化配列のための特殊メソッドを持つ関数のリスト
    "Summary"Datasetとして表された要約情報
  • Normal[CauchyMatrix[x]]はコーシー行列を通常の行列として与える．
  • CauchyMatrix[…,TargetStructure->struct]は，コーシー行列を struct で指定された形式で返す．以下はその可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Structured"行列を構造化配列として表す
    "Symmetric"行列を対称行列として表す
  • CauchyMatrix[…,TargetStructureAutomatic]はCauchyMatrix[…,TargetStructure"Structured"]に等しい．

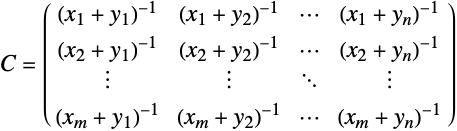
例題

すべて開くすべて閉じる

例  (2)

コーシー行列を構築する：

要素を表示する：

NormalはCauchyMatrixを通常の表現に変換することができる：

記号要素で密なコーシー行列を構築する：

要素を表示する：

行列式を得る：

スコープ  (6)

対称コーシー行列を生成する：

要素を表示する：

通常の表現を得る：

矩形コーシー行列を生成する：

要素を表示する：

通常の表現を得る：

コーシー行列を構造化配列として表す：

要素を表示する：

通常．構造化表現は使用メモリがはるかに少ない：

CauchyMatrixオブジェクトは配列についての情報を与える特性を含んでいる：

"XVector"特性と"YVector"特性はコーシー行列の生成ベクトルを与える：

"Summary"特性は配列についての情報の簡単な要約を与える：

"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数のリストを与える：

構造化アルゴリズムは，適切な場合は，別のCauchyMatrix oオブジェクトを返す：

転置もまたCauchyMatrixである：

コーシー行列とその転置の積はもはやコーシー行列ではない：

オプション  (1)

TargetStructure  (1)

コーシー行列を密な行列として返す：

コーシー行列を構造化配列として返す：

コーシー行列を対称行列として返す：

アプリケーション  (3)

ヒルベルト(Hilbert)行列をCauchyMatrixとして表す：

HilbertMatrixと比較する：

大きいヒルベルト行列の逆行列を数値計算する：

構造化バージョンからの結果の方が正確である：

CauchyMatrixを使って固定の極を持つ補間有理関数についての係数を計算する：

有理関数を構築する：

補間式を複素平面上で可視化する：

有理補間が指定されたすべての点を通ることを確認する：

Parter行列をCauchyMatrixとして定義する：

Parter行列はコーシー行列でもありToeplitz行列でもある：

Parter行列の支配特異値は の周りにクラスタ化している：

特性と関係  (2)

コーシー行列を対角行列，Vandermonde行列およびそれらの逆行列の積として表す：

コーシー行列を対角行列，Vandermonde行列，ハンケル(Hankel)行列の積として表す：

考えられる問題  (3)

文献によってコーシー行列の定義が異なり，2番目の生成ベクトルが否定されていることがある：

生成ベクトルの中に反復要素がある場合はコーシー行列は構築できない：

生成ベクトルの中に成分が他の生成ベクトルの成分の否定であるものがある場合はコーシー行列は構築できない：

Wolfram Research (2022), CauchyMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/CauchyMatrix.html （2024年に更新）.

テキスト

Wolfram Research (2022), CauchyMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/CauchyMatrix.html （2024年に更新）.

CMS

Wolfram Language. 2022. "CauchyMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/CauchyMatrix.html.

APA

Wolfram Language. (2022). CauchyMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CauchyMatrix.html

BibTeX

@misc{reference.wolfram_2024_cauchymatrix, author="Wolfram Research", title="{CauchyMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CauchyMatrix.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cauchymatrix, organization={Wolfram Research}, title={CauchyMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/CauchyMatrix.html}, note=[Accessed: 23-November-2024 ]}