WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

Csch

z の双曲線余割を与える．

詳細

記号操作・数値操作の両方に適した数学関数である．
1/Sinh[z]は自動的にCsch[z]に変換される．分解するにはTrigFactorList[expr]を使う．
特別な引数の場合，Cschは自動的に厳密値を計算する．
Cschは任意の数値精度で評価できる
Cschは自動的にリストに縫い込まれる． »
CschはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

予備知識

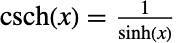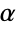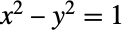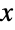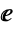Cschは，双曲線余割関数である．これは，三角法で頻繁に使われる，Csc円関数の双曲線バージョンのようなものである．これは，双曲線正弦関数の逆数として，と定義される．これは，実数について，の面積が，単位双曲線と交わる原点からの放射線と軸との間の面積の2倍になるようにすることで定義される．そうすると，Csch[α]は交点の垂直座標の逆数を表す．Cschはとしても定義される．ただし，は自然対数Logの底である．
Cschは，その引数が有理数の（自然）対数であるときは，自動的に厳密値に評価される．引数として厳密な数式が与えられると，Cschは任意の数値精度に評価されることがある．TrigFactorListを使って，Cschを含む式をSinh，Cosh，Sin，Cosを含む項に因子分解することができる．Cschを含む記号式の操作に便利なその他の演算には，TrigToExp，TrigExpand，Simplify，FullSimplifyがある．
Cschは要素単位でリストおよび行列に縫い込まれる．対照的に，個々の行列要素の双曲線余割とは違って，MatrixFunctionは正方行列の双曲線余割（つまり，通常のベキが行列のベキで置き換えられた双曲線余割関数のベキ級数）を与えるのに使うことができる．
Csch[x]は，x が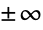に近付くにつれて，指数的に減少する．Cschは，Cscによって満足されるような，ピタゴラス(Pythagorean)の恒等式に似た恒等式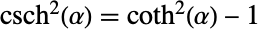を満足する．双曲線余割関数の定義は，恒等式によって，複素引数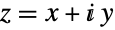にまで拡張される．Cschは整数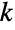について値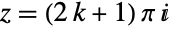において極を持ち，これらの点で評価するとComplexInfinityになる．Csch[z]は，原点付近で級数展開 $sum_(k=0)^infty(2(2^(2 k-1)-1) TemplateBox[{{2, , k}}, BernoulliB] )/((2 k)!)z^(2 k-1)$ を持つ．これはベルヌーイ(Bernoulli)数BernoulliBによって表すことができる．
Cschの逆関数はArcCschである．他の関連する数学関数にはSinhおよびSechがある．

例題

すべて開くすべて閉じる

例 (5)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

特異点における漸近展開：

スコープ (47)

数値評価 (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素引数について評価する：

Cschを高精度で効率よく評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のCsch関数を計算することもできる：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

特定の値 (5)

固定された純粋な虚点におけるCschの値：

無限大における値：

Cschの特異点：

方程式を満足するの値を求める：

値を代入する：

結果を可視化する：

簡単な厳密値は自動的に生成される：

より複雑な場合には明示的にFunctionExpandを使用する必要がある：

可視化 (3)

Csch関数をプロットする：

の実部をプロットする：

の虚部をプロットする：

の極プロット：

関数の特性 (12)

実数上のCschの領域：

複素領域：

Cschは0以外のすべての実数値に達する：

Cschは奇関数である：

Cschは鏡特性を有する：

Cschは解析関数ではない：

しかし，有理型である：

Cschは非減少でも非増加でもない：

Cschは単射である：

Cschは全射ではない：

Cschは非負でも非正でもない：

Cschは零点に特異点と不連続点の両方を持つ：

Cschは凸でも凹でもない：

TraditionalFormによる表示：

微分 (3)

一次導関数：

高次導関数：

次導関数の式：

積分 (3)

Cschの不定積分：

原点を中心とした区間上の奇関数の定積分は0である：

その他の積分例：

級数展開 (3)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りのCschの最初の3つの近似をプロットする：

Cschの級数展開における一般項：

Cschはベキ級数に適用できる：

積分変換 (2)

LaplaceTransformを使ってラプラス(Laplace)変換を計算する：

FourierTransform：

関数の恒等式と簡約 (6)

倍角のCsch：

総和のCsch：

マルチアングルの式を変換する：

双曲線関数の総和を積に変換する：

実変数およびを仮定して展開する：

指数関数に変換する：

関数表現 (4)

Sinを介した表現：

ベッセル(Bessel)関数を介した表現：

ヤコビ関数を介した表現：

MeijerGによる表現：

アプリケーション (3)

複素平面上で絶対値をプロットする：

ポアンソ(Poinsot)の渦巻きをプロットする：

微分方程式を解く：

特性と関係 (9)

Cschの基本的なパリティと周期性の特性は自動的に適用される：

SimplifyとFullSimplifyを使ってCschを含む式を簡約する：

FunctionExpandを使って累乗根における特別な値を表現する：

逆関数を使って構成する：

双曲型方程式を解く：

超越方程式の根を数値的に求める：

総和，積，微分方程式からCschを得る：

Cschは特殊関数の特殊なケースに見られる：

Cschは数値関数である：

考えられる問題 (5)

機械精度の入力は正しい答を出すのには不十分である：

代りに任意精度で評価する：

$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

Cschの逆関数を評価するとSinhになる：

Cschが真性特異点を持つ無限大にはベキ級数は存在しない：

TraditionalFormでは引数の前後に丸カッコが必要である：

おもしろい例題 (1)

無限大でCschをプロットする：

トップへ