DifferenceRoot

DifferenceRoot[lde][k]

線形差分方程式 lde[h,k]で指定されたホロノミック数列 を与える．

DifferenceRoot[lde]

純ホロノミック数列 を与える．

詳細

  • 記号操作と数値操作の両方に適した数学的数列である．ホロノミック数列およびP再帰数列としても知られている．
  • DifferenceRoot関数で定義されるホロノミック数列 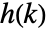は，多項係数 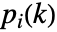を持ち，初期値が 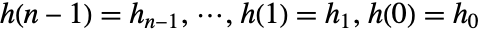の，ホロノミック差分方程式 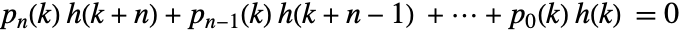を満足する．
  • DifferenceRootは他の任意の数学関数と同じように使うことができる．
  • FunctionExpandはDifferenceRoot関数を特殊関数によって変換しようとする．
  • DifferenceRootで表される数列には，多くの特殊数列が含まれる．
  • DifferenceRootReduceは多くの特殊数列をDifferenceRoot数列に変換することができる．
  • ホロノミック数列は，以下を含む多くの操作の下で閉じている．
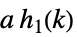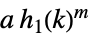
  • , 定数倍，整数ベキ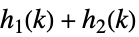
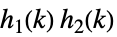
    , 和と積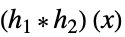
    離散たたみ込み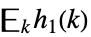
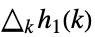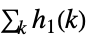
    , , 離散シフト，差と和
  • DifferenceRootは，Sum，RSolve，SeriesCoefficient等の関数によって，自動的に生成される．
  • Sum，DifferenceDelta，GeneratingFunction等の関数には，DifferenceRoot入力を使うことができる．
  • DifferenceRootは自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (2)

fがフィボナッチ(Fibonacci)数列であると定義する：

20番目のフィボナッチ数を計算する：

結果を組込みのFibonacci関数と比較する：

最初の10個のフィボナッチ数をプロットする：

最初の30個のフィボナッチ数の和を計算する：

フィボナッチ数列の母関数 を求める：

の級数展開の最初の10個の係数を求める：

結果を最初の10個のフィボナッチ数と比較する：

関数の中にはDifferenceRoot関数を使って閉形式の答を作ることができるものもある：

スコープ  (21)

数値評価  (6)

DifferenceRoot数列を定義する：

任意の点で評価する：

数列を非厳密な係数で評価する：

数列を複素係数で評価する：

数列をパラメータで評価する：

数列を負の項について評価する：

DifferenceRootは要素単位でリストと行列に縫い込まれる：

可視化  (2)

f というDifferenceRootオブジェクトを定義する：

f の最初の10項をプロットする：

f の最初の25項をListLinePlotを使ってプロットする：

f というDifferenceRootオブジェクトを定義する，パラメータ a は任意でもよい：

数列 f をパラメータ a のさまざまな値についてプロットする：

関数の特性  (9)

DifferenceRootは，線形再帰方程式に使うことができる：

DifferenceRootは，有理係数を持つ再帰方程式を多項式係数を持つ形に変換する：

非同次再帰方程式は，より高次の同次再帰方程式に変換される：

DifferenceRootは多項式強制関数を持つ非同次方程式に使うことができる：

非同次数列の最初の10項を計算する：

DifferenceRootは複数の初期値で使うことができる：

記号成分を持つ数列についての差分関数：

がInfinityに近付くときのDifferenceRootオブジェクトの最高次の漸近項を求める：

AsymptoticRSolveValueを使って同じ結果を得る：

DifferenceRootはパラメータを取ることができる：

この数列の最初の5つの項を記号的な a について計算する：

パラメータ a を指定する：

数列 f をパラメータ a のさまざまな値についてプロットする：

可能な場合は，DifferenceRootは組込み関数に縮退する：

特殊数列  (3)

Fibonacciからの差分方程式：

LucasLからの差分方程式：

HarmonicNumberからの差分方程式：

微分  (1)

ChebyshevT多項式に対応するパラメトリック数列を生成する：

この数列のパラメータについての導関数を計算する：

ChebyshevTの導関数が従う差分方程式を抽出する：

この数列の最初の10項とChebyshevTの直接導関数の等価性をチェックする：

一般化と拡張  (2)

ホロノミックな定数項を持つ方程式は自動的に多項式係数に上げられる：

次の関数は n>0については定義されない：

すべての n について定義されるように初期値 y[1]=2を加える：

アプリケーション  (6)

DifferenceRootを使ってHarmonicNumberの差分方程式形式を得る：

特殊数列の組合せを簡約してDifferenceRoot形式にする：

f を任意の数列にように使う：

DifferenceRootを使ってペル(Pell)数列を定義する：

これを任意の数列のように使う：

ペル数の特性を証明する：

閉じた形の式：

総和恒等式：

特殊数列の組合せを簡約してDifferenceRootにする：

これをプロットする：

テイラー(Taylor)展開が与えられたDifferenceRootオブジェクトである関数を生成する：

結果を検証する：

BesselJ 関数を生成するDifferenceRootオブジェクトを生成する：

特性と関係  (14)

DifferenceRootReduceを使ってDifferenceRootオブジェクトを生成する：

対応する常差分方程式を得る：

この方程式を使って解を証明する：

DifferenceRootオブジェクトの総和：

GeneratingFunctionは，ホロノミック数列からDifferentialRootオブジェクトを生成することがある：

特別なケースについては，GeneratingFunctionが明示的な関数を与えるかもしれない：

DifferenceRootオブジェクトの指数母関数を求める：

差分方程式の解はDifferenceRootオブジェクトかもしれない：

Sumからの結果はDifferenceRootオブジェクトかもしれない：

関数を展開した際の係数はDifferenceRootオブジェクトとして与えられるかもしれない：

FindSequenceFunctionからの結果はDifferenceRootオブジェクトかもしれない：

FunctionExpandはDifferenceRootについてより簡単な式を生成しようとする：

FunctionExpandはパラメトリック数列についてより簡単な式を生成しようとする：

f がホロノミック数列であると定義する：

結果をRecurrenceTableの出力と比較する：

DiscreteShiftはDifferenceRoot関数を取ってシフトされた数列を生成する：

DifferenceDeltaはDifferenceRoot関数を入力として取る：

この式を簡約する：

考えられる問題  (2)

DifferenceRootは多項式係数がある線形微分方程式しか評価しない：

DifferenceRootは整数項しか評価しない：

おもしろい例題  (1)

DifferenceRoot関数を定義する：

これをプロットする：

恒等式を証明する：

展開してあまり一般的ではない関数にしようとする：

Wolfram Research (2008), DifferenceRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferenceRoot.html （2020年に更新）.

テキスト

Wolfram Research (2008), DifferenceRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferenceRoot.html （2020年に更新）.

CMS

Wolfram Language. 2008. "DifferenceRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/DifferenceRoot.html.

APA

Wolfram Language. (2008). DifferenceRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferenceRoot.html

BibTeX

@misc{reference.wolfram_2024_differenceroot, author="Wolfram Research", title="{DifferenceRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DifferenceRoot.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_differenceroot, organization={Wolfram Research}, title={DifferenceRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/DifferenceRoot.html}, note=[Accessed: 23-November-2024 ]}