DiscreteInputOutputModel

DiscreteInputOutputModel[{g0,g1,…,gn-1},u]

入力 u，サンプリングインスタン i とにおける出力 の離散時間モデルを表す．

DiscreteInputOutputModel[{g0,g1,…,gn-1},u,y]

出力変数 y にも依存する出力 の指定に使うことができる．

DiscreteInputOutputModel[…,{{u1,{…,u10}},…},{{y1,{…,y10}},…}]

インスタント k<=0の各信号についての入出力値を指定する．

詳細とオプション

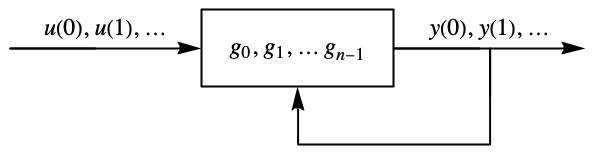
  • DiscreteInputOutputModelは等間隔のサンプリングインスタントにおける出力が系の入力と直前の出力の関数である系を表す．
  • DiscreteInputOutputModelを使って，離散時間TransferFunctionModelオブジェクトを含む入出力形式で離散時間系を表すことができる．これは，通常，ModelPredictiveControllerで計算されたMPCコントローラを表すために使われる．
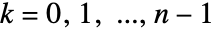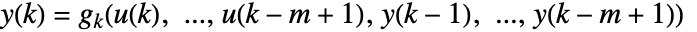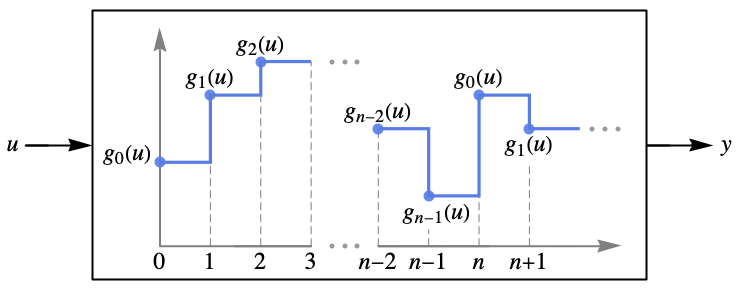
  • 以下の入出力モデルは について に従う過去の入出力の長さ m の移動窓を表している．
  • k=n,…のとき，この方程式は 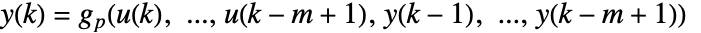および p=TemplateBox[{k, n}, Mod] で周期的に拡張される．
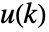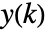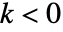  • デフォルトで，入力 と出力 ()は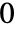であると仮定される．
  • モデル予測制御では2つの単純なケースがよく使われる．
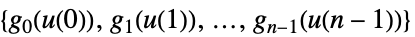
  • 状態フィードバックコントローラ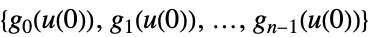
    状態擬似フィードバックコントローラ
  • サンプリングインスタンス間の値は，デフォルトで，一定であるとみなされる．これは，本質的に，補間次数が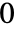のゼロ次ホールド (ZOH) である．
  • 整数サンプリングインスタンス kiと出力 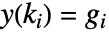はDiscreteInputOutputModel[{{k0,g0},…,{kn-1,gn-1}},…]として明示的に指定できる．
  • 時点 tiはサンプリングインスタンス kiと ti=τ kiの関係にある．ここで，τ はDiscreteInputOutputModel[…, SamplingPeriodτ]として指定されたサンプリング周期である．
  • DiscreteInputOutputModel["prop"]は特性の計算に使うことができる．
  • 次は，出力指定{ki,gi}に関連する特性である．
  • "FirstInstant"最初のインスタントMin[{k0,k1,…}]
    "FirstValue"最初のインスタントにおける値
    "Instants"サンプリングインスタントSort[{k0,k1,…}]
    "LastInstant"最後のインスタントMax[{k0,k1,…}]
    "LastValue"最後のインスタントにおける値
    "Path"インスタントと値のペア{{k0,g0},…}
    "PathComponent"最初のパス要素
    "PathComponents"単変数成分に分解されたすべてのパス
    "PathFunction"補間されたパス関数
    "PathLength"パスの長さ("Horizon")
    "Values"出力値{g0,g1,…}
  • 次は，基本的なモデル特性である．
  • "InputsCount"入力数
    "InputVariables"入力変数 u
    "OutputsCount"出力数
    "OutputVariables"出力変数 y
    "Type"入出力関係の型
    "SamplingPeriod"サンプリング周期 sp
  • 次は，時系列の特性である．
  • "FirstTime"最初のインスタントに対応する時点
    "LastTime"最後のインスタントに対応する時点
    "TemporalData"マルチパスのTemporalDataオブジェクト
    "TimePath"インスタントと値のペア{{t0,g0},…}
    "Times"サンプリングインスタントに対応する時点
    "TimeSeries"TimeSeriesオブジェクト
    "TimeValues"サンプリングの時点に対応する出力値
  • DiscreteInputOutputModelは以下のオプションを取る．
  • MissingDataMethod None欠落値に使用するメソッド
    ResamplingMethod {"Interpolation", InterpolationOrder0}パスのリサンプリングに使用するメソッド
    SamplingPeriod Automaticサンプリング周期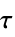

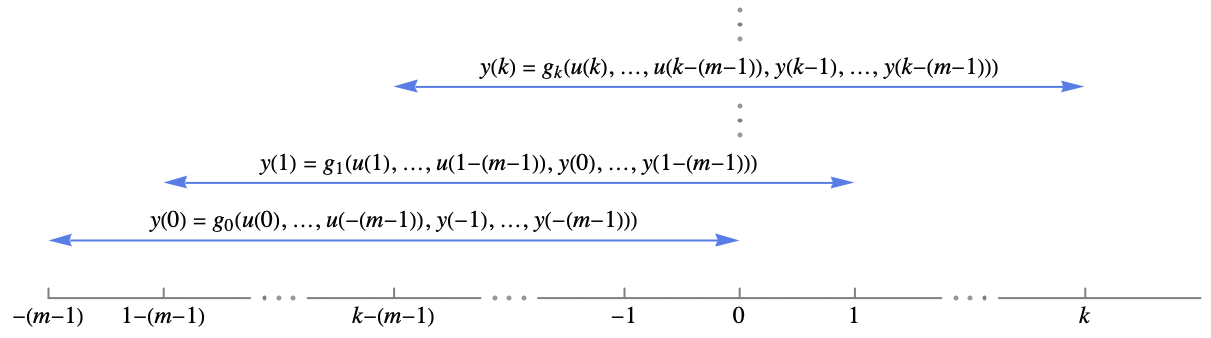
例題

すべて開くすべて閉じる

例  (3)

出力が入力のみに依存するモデル：

ランダムな入力列に対する応答：

出力が入力と出力のみに依存するモデル：

正弦波入力に対する応答：

非零の初期条件を持つモデル：

ランプのような入力列に対する応答：

非零の初期条件を持つ応答は異なる：

スコープ  (30)

基本的な用法  (8)

出力が現行の入力値である系：

その出力は入力と同じである：

入力列が長くなるほど出力は周期性を考慮して計算される：

出力が直前と現行の入力の平均である系：

出力が直前の出力と現行入力の平均である系：

実行中の最大値を計算する系：

FoldListを使って同じ結果を得る：

実行中の最大値と最小値を計算する複数出力の系：

FoldListを使って同じ結果を得る：

非零の初期値を指定する：

負の入力集合に対する応答：

正の入力集合に対する応答：

デフォルト値が0のモデル：

負の有力に対しては最大値が常に誤って0になる：

正の入力に対しては，最小値が誤って常に0になる：

周期性が3の二出力系：

そのランプ入力に対する応答：

一連の区分出力がある系：

ランダム入力に対するその応答：

TransferFunctionModel  (4)

一入力一出力(SISO)の系のTransferFunctionModel：

同等のDiscreteInputOutputModel：

応答は等しい：

多入力多出力(MISO)の系のTransferFunctionModel：

同等のDiscreteInputOutputModel：

応答は等しい：

一入力多出力(SIMO)の系のTransferFunctionModel：

同等のDiscreteInputOutputModel：

応答は等しい：

多入力多出力(MIMO)の系のTransferFunctionModel：

同等のDiscreteInputOutputModel：

応答は等しい：

ModelPredictiveController  (2)

ModelPredictiveController設計のフィードバックゲインモデル：

フィードバックゲインは状態の一連の区分関数である：

擬似フィードバックゲインモデルもまたDiscreteInputOutputModelである：

これは時点0における状態の一連の区分関数である：

多入力ModelPredictiveController設計のフィードバックゲインモデル：

区分関数の値は2入力に対応して長さ2である：

特性  (16)

モデルの中のすべての値を得る：

最初の値：

最後の値：

特定のインスタントにおける値：

すべてのインスタント：

最初のインスタント：

最後のインスタント：

インスタントと値のペアのリスト：

多変数のパスを単変量の成分に分割する：

最初の成分のパス：

2番目の成分のパス：

"PathComponent"は最初の成分を与える：

2番目の成分を得る：

いくつかの成分を得る：

補間されたパス関数：

パスの長さ：

基本的なモデルの特性：

時点で指定された特性：

複数の特性をリストとして得る：

すべての特性をAssociationとして得る：

すべての特性をDatasetとして得る：

オプション  (3)

MissingDataMethod  (1)

欠落値の扱い方を指定する：

ResamplingMethod  (1)

デフォルトのリサンプリングメソッドの補間次数は0である：

補間次数1を指定する：

補間次数が1のときの値：

SamplingPeriod  (1)

デフォルトのサンプリング周期は1である：

サンプリングインスタントと時間は一致するので，"Path"と"TimePath"は同じ結果を与える：

"TimePath"は"TimeSeries"の"Path"からも得えられる：

サンプリング周期が2の系：

"Path"はサンプリングインスタントによるが，"TimePath"は時点の値による：

アプリケーション  (3)

ローパスFIRカーネルを計算する：

これをDiscreteInputOutputModelとして組み立てる：

ノイズのある正弦波に対する応答を計算する：

ListConvolveを使っても同じ結果が得られる：

2つの応答は，実際に等しい：

IIRフィルタの距離の近似を計算する：

これをDiscreteInputOutputModelとして組み立てる：

ノイズのある正弦波入力に対する応答を計算する：

アナログのTransferFunctionModel表現はほぼ同じ応答を与える：

MPC設計についてフィードバックゲインモデルと閉ループ系を計算する：

フィードバックゲインモデルは離散入出力モデルで閉ループ系の一部である：

閉ループ系のシミュレーションを行う：

特性と関係  (4)

たたみ込みを形成する：

ListConvolveは同じ結果を与える：

線形回帰方程式：

DiscreteInputOutputModelを使ってこれを表す：

入力列に対する応答：

RecurrenceFilterも同じ結果を与える：

離散TransferFunctionModel表現のある過程：

これはDiscreteInputOutputModel表現も持つ：

応答は等しい：

DiscreteInputOutputModelは入出力変数がなければ基本的にTimeSeriesである：

同等のTimeSeriesオブジェクト：

そのパス：

時系列を特性として得る：

これも同じパスを持つ：

時間のパスも同様に直接得ることができる：

考えられる問題  (2)

時系列を得ることで指定がサンプリングインスタントからタイムスタンプに変わることがある：

サンプリングインスタント1における値：

同等の時系列を計算する：

時系列はサンプリングインスタントによるものではない：

同等のタイムスタンプを使う：

時系列のパス：

もとのモデルからの時系列のパスは等しい：

しかし，もとのもでるのパスはサンプリングインスタントによるものである：

初期値 と は系の応答の計算には使われない：

Wolfram Research (2022), DiscreteInputOutputModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

テキスト

Wolfram Research (2022), DiscreteInputOutputModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

CMS

Wolfram Language. 2022. "DiscreteInputOutputModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

APA

Wolfram Language. (2022). DiscreteInputOutputModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html

BibTeX

@misc{reference.wolfram_2024_discreteinputoutputmodel, author="Wolfram Research", title="{DiscreteInputOutputModel}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discreteinputoutputmodel, organization={Wolfram Research}, title={DiscreteInputOutputModel}, year={2022}, url={https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html}, note=[Accessed: 23-November-2024 ]}