DiskSegment

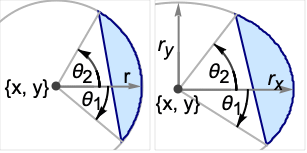
DiskSegment[{x,y},r,{θ1,θ2}]

表示圆盘中从角度 θ1 到 θ2 的圆盘弓形，该圆盘以 {x,y} 为中心，半径为 r.

DiskSegment[{x,y},{rx,ry},{θ1,θ2}]

表示以轴对齐的椭圆中从角度 θ1 到 θ2 的椭圆弓形，该椭圆的半轴长度为 rx 和 ry.

更多信息和选项

  • DiskSegment 可用作几何区域和图形基元.
  • DiskSegment 表示具有相同参数的 Disk 的实心弓形部分.
  • 角度按照从正 x 方向逆时针的弧度单位测量.
  • DiskSegment 可用在 Graphics 里.
  • 在图形中，点 {x,y} 可以是 Dynamic 表达式.
  • 图形绘制受诸如 FaceForm、EdgeForm 及颜色这样的指令影响.

范例

打开所有单元关闭所有单元

基本范例  (5)

单位圆盘的一半：

圆盘弓形：

椭圆圆盘的弓形：

不同样式的圆盘弓形：

获取圆盘弓形（一半的圆盘）的 Area：

椭圆弓形的面积：

范围  (17)

图形  (7)

规范  (4)

指定半径：

指定中心：

指定角度：

椭圆圆盘弓形：

样式  (2)

颜色指令指定圆盘弓形的面颜色：

FaceForm 和 EdgeForm 可用于指定内部和边界的样式：

圆盘弓形的边界：

坐标  (1)

点可以是 Dynamic：

区域  (10)

嵌入维度：

几何维度：

点成员检验：

获取点成员的条件：

面积：

中心：

到一个点的距离：

到一个点的符号距离：

区域中的最近点：

最近点：

椭圆弓形是有界的：

获取它的范围：

圆盘弓形上求积分：

在椭圆弓形上求最优化：

求椭圆弓形中的方程：

应用  (5)

在圆盘弓形上绘制函数图线：

使用 RegionProduct 创建三维圆盘弓形立体图形：

为了显示圆盘和正多边形之间的区域差值，可以使用圆盘弓形的集合. 首先，获取弧的集合：

但是，一些弧不是递增的角度范围，因此在这些情况下，把 添加到第二个角度使其递增：

最后，可视化：

透镜可以建模为两个相邻的圆盘弓形. 创建高度为 ，半径为 的朝右的透镜弓形，以原点为中心：

对于朝左的透镜，您必须转变 位置并且转变弧的方向：

现在创建一个函数构建给定高度和半径的圆盘弓形对，并且对一定半径范围值可视化：

通过查询位于已知体积的区域中的随机点的比率，您可以找到区域的近似测量值. 将圆盘花瓣作为示例使用：

该区域可以包含在区域 和 中，它的面积为16. 产生这个普通区域中的随机点列表：

求位于圆盘花瓣中的这些随机点的百分比：

区域（圆盘花瓣）的面积应该接近比率乘以随机点分布的面积. 将该近似值与实际值比较：

属性和关系  (4)

DiskSegment 可以用 FilledCurve 表示：

圆盘弓形可以从 Disk 的 RegionIntersection 和另一个区域获得：

ImplicitRegion 可以表示任意 DiskSegment：

ParametricRegion 可以表示 DiskSegment：

巧妙范例  (3)

随机圆盘弓形集合：

圆盘弓形组成的系列：

数字花瓣：

Wolfram Research (2015)，DiskSegment，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiskSegment.html.

文本

Wolfram Research (2015)，DiskSegment，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DiskSegment.html.

CMS

Wolfram 语言. 2015. "DiskSegment." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiskSegment.html.

APA

Wolfram 语言. (2015). DiskSegment. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiskSegment.html 年

BibTeX

@misc{reference.wolfram_2024_disksegment, author="Wolfram Research", title="{DiskSegment}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DiskSegment.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_disksegment, organization={Wolfram Research}, title={DiskSegment}, year={2015}, url={https://reference.wolfram.com/language/ref/DiskSegment.html}, note=[Accessed: 21-November-2024 ]}