EigenvectorCentrality

EigenvectorCentrality[g]

グラフ g 中の頂点の固有ベクトル中心性のリストを与える．

EigenvectorCentrality[g,"In"]

有向グラフ g の入中心性のリストを与える．

EigenvectorCentrality[g,"Out"]

有向グラフ g の出中心性のリストを与える．

EigenvectorCentrality[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • EigenvectorCentralityは数多くの頂点と連結している頂点と多数連結している頂点に高い中心性を与える．
  • EigenvectorCentralityは近傍の中心性の重み付き総和として表すことができる中心性 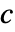のリストを与える．
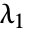  • がグラフ g の隣接行列 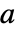の最大固有値のときは次のようになる．
  • EigenvectorCentrality[g]c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c
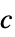    EigenvectorCentrality[g,"In"]c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c, 左固有ベクトル
    EigenvectorCentrality[g,"Out"]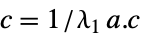, 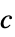右固有ベクトル
  • 固有ベクトルの中心性は正規化される．
  • 有向グラフ g については，EigenvectorCentrality[g]はEigenvectorCentrality[g,"In"]と等価である．
  • オプションWorkingPrecision->p を使って内部計算で使われる精度が制御できる．
  • EigenvectorCentralityは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

例題

すべて開くすべて閉じる

例  (2)

固有ベクトル中心性を計算する：

ハイライトする：

頂点に順位を付ける．順位が最も高い頂点はたくさんの連結を持つ多くの頂点に連結されている：

スコープ  (7)

EigenvectorCentralityは無向グラフに使うことができる：

有向グラフに使う：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

入中心性と出中心性を計算する：

EigenvectorCentralityは大きいグラフに使うことができる：

オプション  (3)

WorkingPrecision  (3)

デフォルトで，EigenvectorCentralityは機械精度計算で中心性を求める：

より高い作業精度を指定する：

無限作業精度は厳密計算に相当する：

アプリケーション  (9)

他のたくさんの接続がある頂点との接続性で頂点をランク付けする：

頂点を中心性の高いものから低いものへと並べる：

CycleGraphの固有ベクトル中心性をハイライトする：

GridGraph：

CompleteKaryTree：

PathGraph：

ソーシャルネットワークでうまく繋がっている人々を求める：

ネットワークをハイライトする：

学生Aが学生Bに意見を求める場合の学生Aから学生Bへの接続から，学生自治会ネットワークで最も影響力の強いメンバーを求める：

arXiv e-Printアーカイブのgh Energy Physics Phenomenologyセクションからの引用ネットワーク．最も引用されている上位10本の論文を求める：

自立システムのレベルでのインターネットのハブを求める：

ハブはたくさんの連結点を持つ頂点で固有ベクトル中心性が最も高いものである：

削除するとイーストのタンパク質相互作用ネットワークに致命的な影響を与えるタンパク質を求める：

固有ベクトル中心性が最大のタンパク質：

このタンパク質を削除するとネットワークの直径が増大する：

「出芽酵母」タンパク質相互作用ネットワーク．固有ベクトル中心性の頻度はベキ法則分布に従う：

パレート(Pareto)分布を仮定して最大尤度母数推定を求める：

確率密度関数：

インターネットで注文を受けて商品を郵送する機関の人間とコンピュータのシステム．最も多くの人員を配備すべき部署を求める：

ほとんどのサービスがシステム管理部と注文管理部に依存している：

特性と関係  (6)

無向グラフの場合，中心性ベクトル は方程式 を満たす：

有向グラフの場合，入中心性ベクトル は方程式 を満たす：

出中心性ベクトル は方程式 を満たす：

固有ベクトル中心性は正規化される：

不連続グラフの場合，中心性は連結成分について正規化される：

連結成分によって生成された部分グラフの中心性：

EigenvectorCentralityはKatzCentralityの特殊ケースである：

と をKatzCentralityのパラメータとして使う：

VertexIndexを使って特定の頂点の中心性を得る：

Wolfram Research (2010), EigenvectorCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/EigenvectorCentrality.html （2015年に更新）.

テキスト

Wolfram Research (2010), EigenvectorCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/EigenvectorCentrality.html （2015年に更新）.

CMS

Wolfram Language. 2010. "EigenvectorCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EigenvectorCentrality.html.

APA

Wolfram Language. (2010). EigenvectorCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EigenvectorCentrality.html

BibTeX

@misc{reference.wolfram_2024_eigenvectorcentrality, author="Wolfram Research", title="{EigenvectorCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eigenvectorcentrality, organization={Wolfram Research}, title={EigenvectorCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}, note=[Accessed: 23-November-2024 ]}