EstimatedVariogramModel
EstimatedVariogramModel[{loc1val1,loc2val2,…}]
根据在位置 loci 处给出的值 vali 估计最佳变异函数.
EstimatedVariogramModel[{loc1,loc2,…}{val1,val2,…}]
产生相同的结果.
EstimatedVariogramModel[…,"model"]
估计由 "model" 指定的变异函数的最佳参数.
EstimatedVariogramModel[…,{"model",params}]
估计 params 中的非数字参数.
更多信息和选项




- 变异函数模型也称为变异函数(variogram)和半变异函数(semivariogram).
- EstimatedVariogramModel 将模型拟合到空间场数据并返回 VariogramModel.
- VariogramModel 在预测空间场的值时,通常用作空间相关性的局部模型,如在 SpatialEstimate 中一样.
- 空间过程
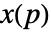 在位置
在位置 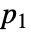 和
和 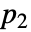 的变异函数
的变异函数 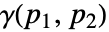 由
由 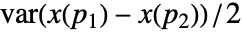 给出. 它是过程在空间上变化速度的度量.
给出. 它是过程在空间上变化速度的度量. - 当过程弱平稳时,变异函数仅取决于位置的差异,即
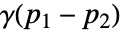 . 而当过程是各向同性时,它只取决于位置之间的距离
. 而当过程是各向同性时,它只取决于位置之间的距离 ![gamma(TemplateBox[{{{p, _, 1}, -, {p, _, 2}}}, Norm]) gamma(TemplateBox[{{{p, _, 1}, -, {p, _, 2}}}, Norm])](Files/EstimatedVariogramModel.zh/8.png) .
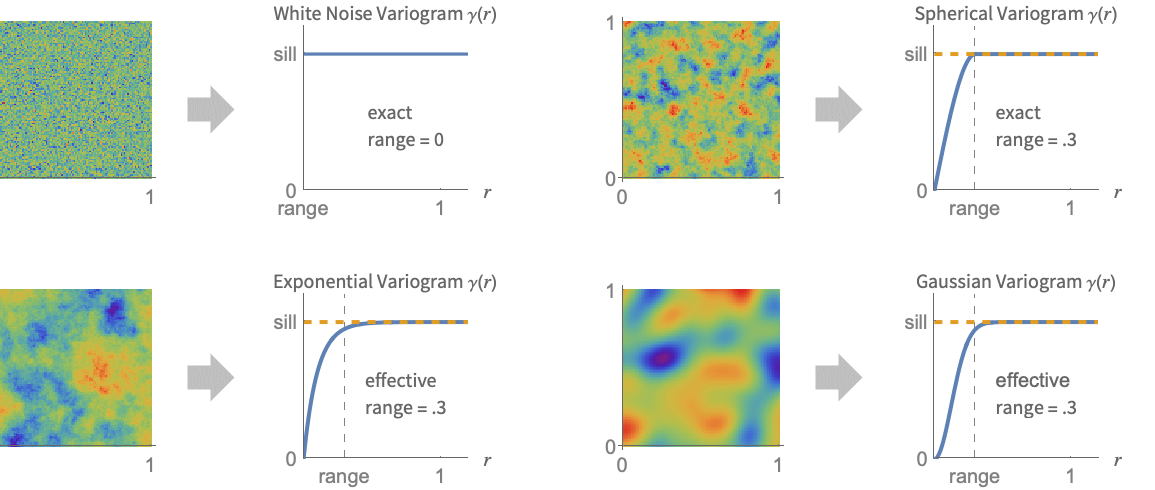
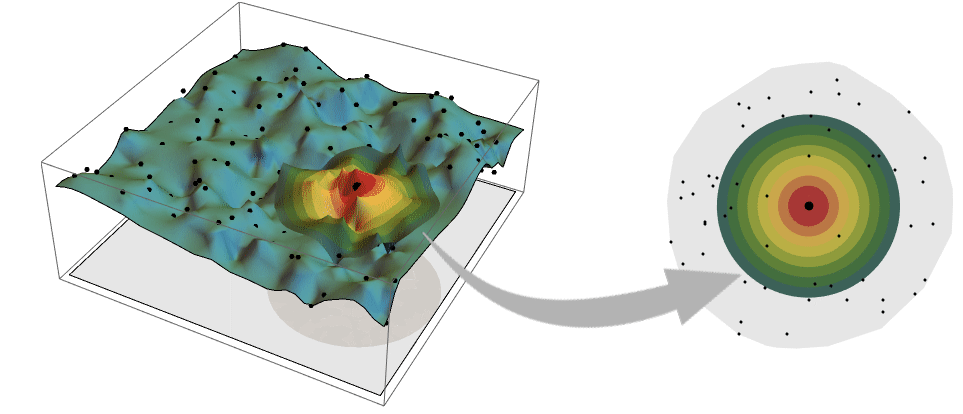
. - 静止且各向同性的空间场数据以及相应的变异函数的典型示例.
- 使用自动设置,这就足够了,但如果想对变异函数模型进行详细控制,还需要了解更多方面. 两个主要问题是平滑的范围和水平.
- 变异函数的范围表示对附近点扩展程度的依赖性. 变异函数的范围越大,对应的场的变化越慢.
-
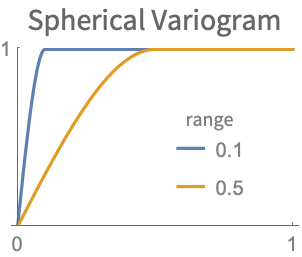

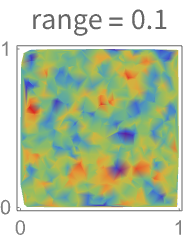
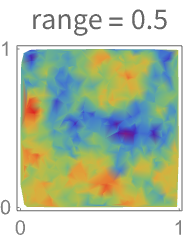
- 变异函数的范围控制距离,在该距离的点影响 SpatialEstimate 中值的预测范围.
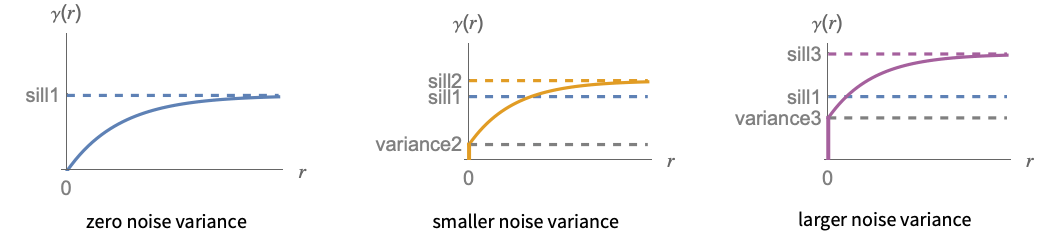
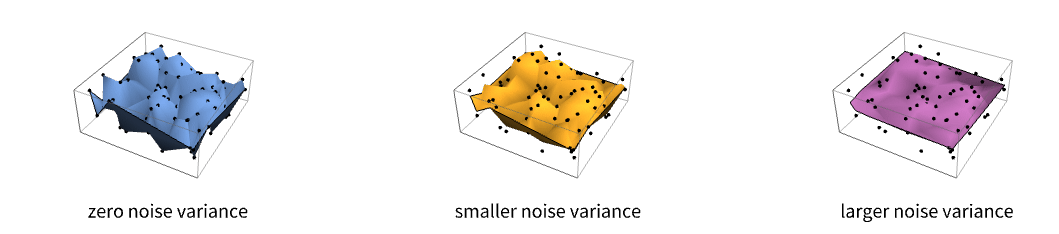
- 预测的平滑度受变异函数的所谓空间噪声方差的影响,该方差是原点处的值. 它对应于添加白噪声模型,例如数据中的测量错误或真正的不连续性,例如块金模型.
- 空间噪声方差的大小控制 SpatialEstimate 中值的平滑级别. 特别地,对于非零噪声方差,生成的表面不会对给定值进行插值,而是对它们进行近似.
- 位置 loci 具有以下形式:
-
{p1,…,pd} 几何位置 GeoPosition[…],GeoPositionENU[…],… 地理位置 - 值 vali 具有以下形式:
-
ci 标量值 Quantity[ci,"unit"] 标量 - 模型需要满足一致性条件才能成为有效的空间变异函数. 它必须是一个非负函数,并且对于所有使得
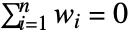 的权值 wi 和位置 pi,满足条件负定条件
的权值 wi 和位置 pi,满足条件负定条件 ![sum_(i=1)^nsum_(j=1)^nw_i w_j gamma(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])<=0 sum_(i=1)^nsum_(j=1)^nw_i w_j gamma(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])<=0](Files/EstimatedVariogramModel.zh/18.png) . 有效的模型族可以分组到具有相似特征的表中,并在 VariogramModel 中列举出来.
. 有效的模型族可以分组到具有相似特征的表中,并在 VariogramModel 中列举出来. - 可以提供以下选项:
-
SpatialNoiseLevel Automatic 指定模型中的噪声方差 SpatialTrendFunction Automatic 指定全局趋势模型

范例
打开所有单元关闭所有单元选项 (3)
SpatialNoiseLevel (1)
SpatialTrendFunction (2)
使用 SpatialTrendFunction 指定趋势函数:
应用 (2)
估计 SpatialPointData 的变异函数模型:
计算 BinnedVariogramList 以了解选择哪个模型系列:
文本
Wolfram Research (2021),EstimatedVariogramModel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html.
CMS
Wolfram 语言. 2021. "EstimatedVariogramModel." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html.
APA
Wolfram 语言. (2021). EstimatedVariogramModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EstimatedVariogramModel.html 年