HistogramTransformInterpolation

HistogramTransformInterpolation[{x1,x2,…}]

変換された値 がほぼ均等に配布されるような関数 を求める．

HistogramTransformInterpolation[{x1,x2,…},ref]

が分布 ref に従って配布されるような関数 を求める．

HistogramTransformInterpolation[{x1,x2,…},ref,n]

等間隔の n 個の分位点を持つ関数を求める．

HistogramTransformInterpolation[image,…]

image のヒストグラムを整形する関数を求める．

詳細

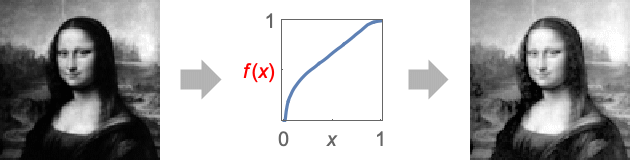
例題

すべて開くすべて閉じる

例  (4)

与えられたデータ集合のサンプルを均等に配布する関数を求める：

データ集合のヒストグラムを正規分布の確率密度関数にマッチするように整形する：

画像のヒストグラムを平坦化する関数を求める：

3D画像のヒストグラムを均質化する関数を求める：

スコープ  (3)

データ集合のリストの平坦化関数を求める：

各カラーチャンネルのヒストグラム整形関数を求める：

チャンネルごとに関数を適用する：

変換関数を求める際に，さまざまな数の変位値を使う：

アプリケーション  (1)

局所的に適応可能なヒストグラムの均質化  (1)

局所的に適応可能なヒストグラムを完全に均質化することで，さまざまな強度レベルを持つ画像ではより魅力的な結果が与えられることがあるが，より長い時間がかかる：

重なり合わないブロックについて計算された均質化関数間の双一次補間の方がより速く近似できる：

特性と関係  (2)

HistogramTransformInterpolationを使ってHistogramTransformで使用する変換関数を求めることができる：

HistogramTransformInterpolationの結果は，閉形式の解が存在する場合はこれを近似する：

Wolfram Research (2012), HistogramTransformInterpolation, Wolfram言語関数， https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html （2014年に更新）.

テキスト

Wolfram Research (2012), HistogramTransformInterpolation, Wolfram言語関数， https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html （2014年に更新）.

CMS

Wolfram Language. 2012. "HistogramTransformInterpolation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html.

APA

Wolfram Language. (2012). HistogramTransformInterpolation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html

BibTeX

@misc{reference.wolfram_2024_histogramtransforminterpolation, author="Wolfram Research", title="{HistogramTransformInterpolation}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_histogramtransforminterpolation, organization={Wolfram Research}, title={HistogramTransformInterpolation}, year={2014}, url={https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html}, note=[Accessed: 21-November-2024 ]}