IsomorphicGraphQ
IsomorphicGraphQ[g1,g2]
更多信息

- IsomorphicGraphQ 也称为图形同构问题.
- IsomorphicGraphQ 通常用于确定两个图形在结构上是否等价.
- 如果对顶点进行重命名可以得到相同的图,则称这两个图是同构的.
- IsomorphicGraphQ[g1,g2,…] 给出 True,如果所有 gi 都是同构的.
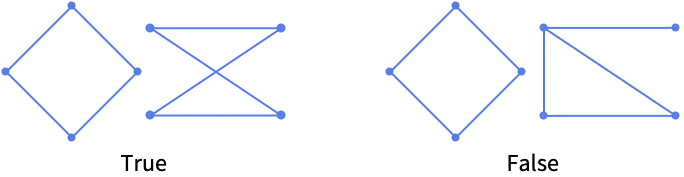
范例
打开所有单元关闭所有单元范围 (4)
属性和关系 (10)
FindGraphIsomorphism 可用于寻找顶点之间的映射关系:
Wolfram Research (2010),IsomorphicGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/IsomorphicGraphQ.html (更新于 2012 年).
文本
Wolfram Research (2010),IsomorphicGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/IsomorphicGraphQ.html (更新于 2012 年).
CMS
Wolfram 语言. 2010. "IsomorphicGraphQ." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2012. https://reference.wolfram.com/language/ref/IsomorphicGraphQ.html.
APA
Wolfram 语言. (2010). IsomorphicGraphQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/IsomorphicGraphQ.html 年