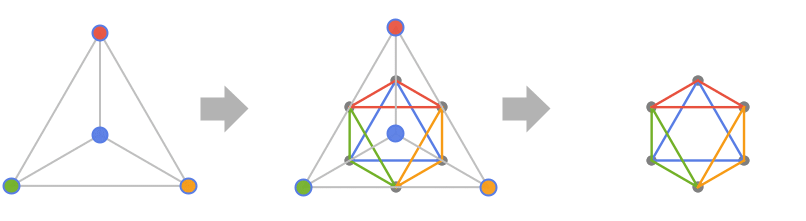
LineGraph
予備知識
- LineGraphは
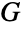 の線グラフ
の線グラフ 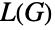 を返す.このグラフは,頂点が
を返す.このグラフは,頂点が 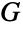 の辺で,頂点隣接性が
の辺で,頂点隣接性が 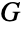 の辺隣接性に相当する.より形式的には,辺が e1,…,emであるグラフ
の辺隣接性に相当する.より形式的には,辺が e1,…,emであるグラフ 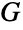 を与えられた場合,
を与えられた場合,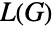 は頂点 e1,…,emを持つことになる.無向グラフ
は頂点 e1,…,emを持つことになる.無向グラフ 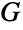 について,
について,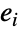 と
と 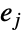 が
が 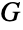 の同じ頂点に接続している場合,
の同じ頂点に接続している場合, は
は 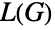 の辺である.一方,有向グラフ
の辺である.一方,有向グラフ 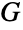 については,
については,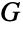 中で
中で 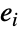 の始点が
の始点が 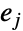 の終点である場合は
の終点である場合は  は
は 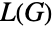 の辺である.線グラフは,随伴グラフ,共役グラフ,被覆グラフ,導関数グラフ,派生グラフ,辺グラフ,辺頂点双対グラフ,交換グラフ,代表グラフ,
の辺である.線グラフは,随伴グラフ,共役グラフ,被覆グラフ,導関数グラフ,派生グラフ,辺グラフ,辺頂点双対グラフ,交換グラフ,代表グラフ,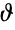 -obrazom グラフと呼ばれることもある.
-obrazom グラフと呼ばれることもある. - 線グラフは,グラフ理論において,グラフ頂点についての結果を辺についての結果に翻訳するために使われる.例えば,
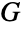 の独立辺集合は
の独立辺集合は 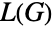 の独立頂点集合になり,
の独立頂点集合になり,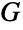 の辺彩色数は
の辺彩色数は 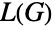 の彩色数と等しい,等である.
の彩色数と等しい,等である. - 線グラフはもとのグラフと数多くの数学的な関係がある.その中でも最も単純なものは,
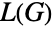 の頂点数が
の頂点数が 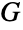 の辺の数と等しいというものである.加えて,
の辺の数と等しいというものである.加えて,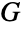 が
が 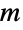 本の辺と
本の辺と 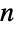 個の頂点を持ち頂点次数が d1,…,dnの単純グラフなら,
個の頂点を持ち頂点次数が d1,…,dnの単純グラフなら,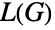 の辺の本数は
の辺の本数は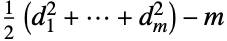 である.線グラフが明示的に構築できるまた別の関係として,単純グラフ
である.線グラフが明示的に構築できるまた別の関係として,単純グラフ 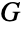 の結合行列
の結合行列 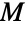 と m×m 恒等行列
と m×m 恒等行列 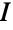 について,
について,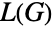 の隣接行列は
の隣接行列は 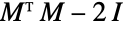 で与えられる.
で与えられる. - あるグラフが線グラフかどうかは線形時間で求めることができる.
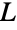 の各頂点が厳密にあるクリーク族のうちの2つのクリークに含まれるようなクリークの族が存在するときかつそのときに限り,グラフ
の各頂点が厳密にあるクリーク族のうちの2つのクリークに含まれるようなクリークの族が存在するときかつそのときに限り,グラフ 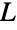 は単純グラフあるいは多重グラフの線グラフであり,
は単純グラフあるいは多重グラフの線グラフであり,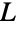 の各辺はそれらのクリークの1つによって誘導される.もし
の各辺はそれらのクリークの1つによって誘導される.もし 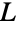 の頂点のうち2つが同じ2つのクリークに含まれないような形でこのクリーク族が形成できるならば,
の頂点のうち2つが同じ2つのクリークに含まれないような形でこのクリーク族が形成できるならば,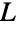 は単純グラフの線グラフである.
は単純グラフの線グラフである. - グラフのそれぞれが最高で6個の頂点を持ち,その単純グラフがその集合中のどのグラフをも誘導部分グラフとして含まないときかつそのときに限り他の単純グラフの線グラフであるような9つの禁止グラフの集合がある.この禁止グラフの集合はGraphData["Beineke"]で与えられ,完全二部グラフ
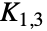 を含むので,線グラフはclaw-freeである.単純グラフのどれの最大次数が少なくとも5であるかを知るためには,これらの禁止グラフのうち6つがあればよい(GraphData["Metelsky"]を参照のこと).
を含むので,線グラフはclaw-freeである.単純グラフのどれの最大次数が少なくとも5であるかを知るためには,これらの禁止グラフのうち6つがあればよい(GraphData["Metelsky"]を参照のこと). - グラフ理論における多くの重要な結果が線グラフの特性を特徴付けている.例えば,Vizingの定理は,
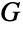 が三角形を含まない単純グラフなら
が三角形を含まない単純グラフなら 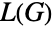 の彩色数は
の彩色数は 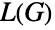 の最大クリーク数と等しいかそれより1大きいことを示唆している.また,Königの線彩色定理は,二部グラフの線グラフ
の最大クリーク数と等しいかそれより1大きいことを示唆している.また,Königの線彩色定理は,二部グラフの線グラフ 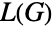 が完全グラフである(つまり,
が完全グラフである(つまり,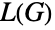 のすべての誘導部分グラフの彩色数が部分グラフの最大クリークのサイズと一致する)ことを示唆している.
のすべての誘導部分グラフの彩色数が部分グラフの最大クリークのサイズと一致する)ことを示唆している.
例題
すべて開くすべて閉じる特性と関係 (11)
おもしろい例題 (1)
Wolfram Research (2010), LineGraph, Wolfram言語関数, https://reference.wolfram.com/language/ref/LineGraph.html (2015年に更新).
テキスト
Wolfram Research (2010), LineGraph, Wolfram言語関数, https://reference.wolfram.com/language/ref/LineGraph.html (2015年に更新).
CMS
Wolfram Language. 2010. "LineGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/LineGraph.html.
APA
Wolfram Language. (2010). LineGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LineGraph.html