ModelPredictiveController

ModelPredictiveController[sspec,cost,cons]

費用関数 cost を最小にして制約条件 cons を満足する系の指定 sspec に従ってモデル予測コントローラを計算する．

ModelPredictiveController[…,"prop"]

特性"prop"の値を返す．

詳細とオプション

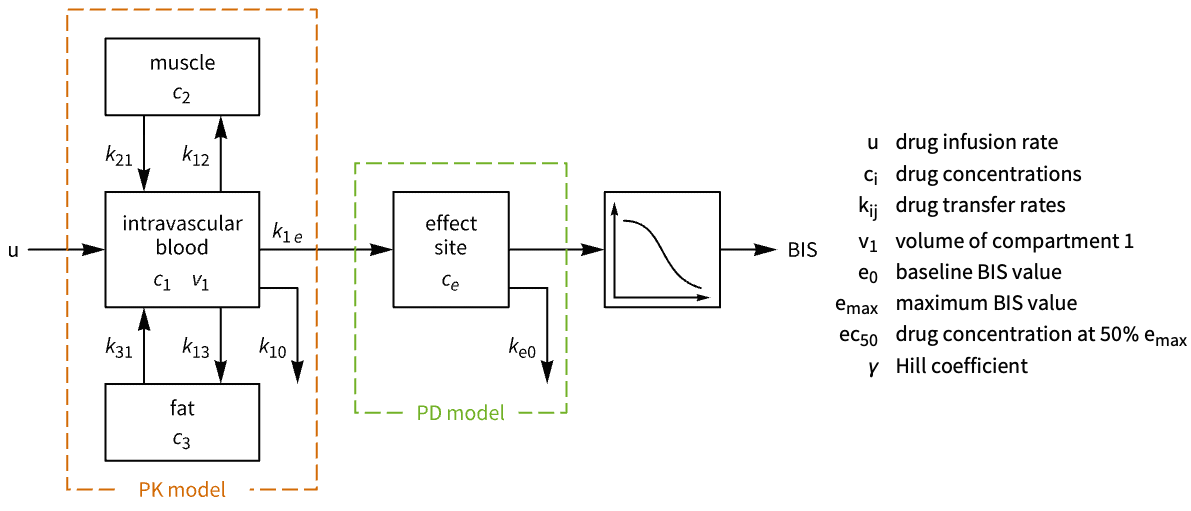
  • モデル予測制御はMPC(model predictive control)としても知られている．
  • モデル予測コントローラは，入力と状態の両方に対する制約を考慮しながら有限の範囲で状態と制御入力の費用関数を最小化することによって計算される．これらの制約は，コントローラの安全な実装を保障するために重要であることが多い．
  • 結果のコントローラーは，単純な区分アフィン形式 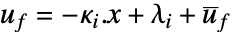を持つ．ここで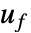， はフィードバック制御入力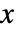， はシステムの状態である．これらはマイクロコントローラに簡単に配備でき，高速プロセスに使用できる．
  • 制御器は，外乱 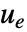がシステムを押しのけようとしても，系を平衡位置に維持することを目的としている．典型的な例には，倒立振子を直立位置に維持することや航空機を水平に維持することが含まれる．
  • MPC制御器は，sspec および制約条件 cons の系のダイナミクス 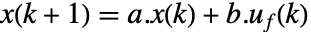に従って費用 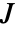を最小にするフィードバックとして指定される．状態 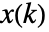とフィードバック制御入力 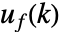の両方が小さくなると費用 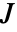も小さくなる．
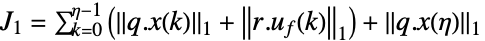
  • 1ノルム，重み付き積分絶対誤差(IAE)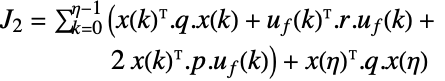
    二乗2ノルム，重み付き積分二乗誤差(ISE)または重み付き「エネルギー」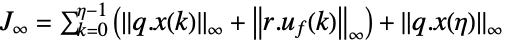
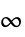    ノルム，重み付きピーク値
  • 費用 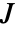は cost Associationで次のキーで指定される．
  • η"Horizon"整数時間範囲
    q"StateWeight"状態についての行列費用
    r"InputWeight"入力についての行列費用
    p"StateInputWeight"相互結合の状態と入力についての列費用
    m"Norm"1，2または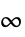
  • 追跡器は外乱 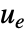があっても参照信号 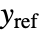の追跡を目的とする．典型的な例としては自動車のクルーズコントロールやロボットの経路追跡がある．
  • MPC追跡器は，sspec と制約条件 cons における系のダイナミクス 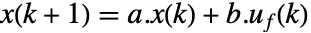に従って費用を最小にするフィードバックとして指定される．予測誤差 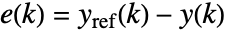と増分するフィードバック制御入力 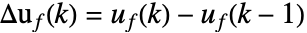の両方が小さくなると費用も小さくなる．
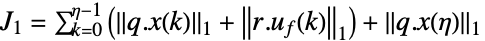
  • 1ノルム，重み付き積分絶対誤差(IAE)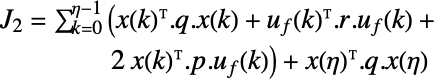
    二乗2ノルム，重み付き積分二乗誤差(ISE)または重み付き「エネルギー」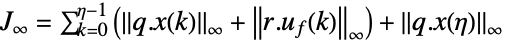
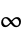    ノルム，重み付きピーク値
  • 費用関数の式の項は以下の通りである．
  • η"Horizon"整数時間範囲
    qe"ErrorWeight"誤差についての行列費用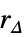
    r_Delta"InputIncrementWeight"増分入力についての行列費用
    peΔ"ErrorInputIncrementWeight"相互結合の状態と入力についての列費用
    m"Norm"1，2または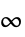
  • 調整器問題と追跡器問題の両方についての制約条件 cons は，状態変数 x，入力変数 u，出力変数 y によって定式化される．これらはStateSpaceModel[{a,b,c,d},x,u,y,…]を使って定義できる．
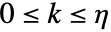  • のとき，特定の時点 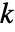で保持される制約．
  • xmin<=xi[k]<=xmax時点 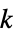における値についての制約
    Δxmin<=xi[k2]-xi[k1]<=Δxmax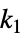時点 から時点 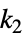までの増分についての制約
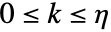  • のとき，すべての時点 k で保持される制約．
  • xmin<=xi<=xmaxすべての k の値についての制約
    min<=α1.x1+…+αn.xn+β<=maxすべての k の線形結合についての制約
    xminxxmaxすべての k のすべての値についての制約
  • 重み行列 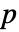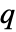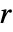，， は以下のように指定できる．
  • q一定の重み{q,…,q,q}
    {{q},qη}さまざまな終端重み{q,…,q,qη}
    {q0,q1,…,qη}さまざまな重み{q0,q1,…,qη}
  • ModelPredictiveControllerはStateSpaceModel[…,SamplingPeriodτ]を使って指定可能な離散時間線形系に使うことができる．
  • 系の指定 sspec は次の形でよい．
  • StateSpaceModel[…]線形制御入力と線形状態
    AffineStateSpaceModel[…]線形制御入力と非線形状態
    NonlinearStateSpaceModel[…]非線形制御入力と非線形状態
    SystemModel[…]一般的な系のモデル
    <|…|>Associationとして与えられる詳細な系の指定
  • 詳細な系の指定は次のキーを持つことができる．
  • "InputModel"sysモデルの任意のもの
    "FeedbackInputs"Allフィードバック入力 uf
    "TrackedOutputs"None追跡された出力 yref
  • フィードバック入力は次の形でよい．
  • {num1,…,numn}StateSpaceModel，AffineStateSpaceModel，NonlinearStateSpaceModelで使われる番号付き入力 numi
    {name1,…,namen}SystemModelで使われる名前付き入力 namei
    Allすべての入力を使う
  • ModelPredictiveControllerは，cd["prop"]を使った追加的な特性の抽出に使われるSystemsModelControllerDataオブジェクト cd を返す．
  • ModelPredictiveController[…,"prop"]を使って cd["prop"]の値を直接得ることができる．
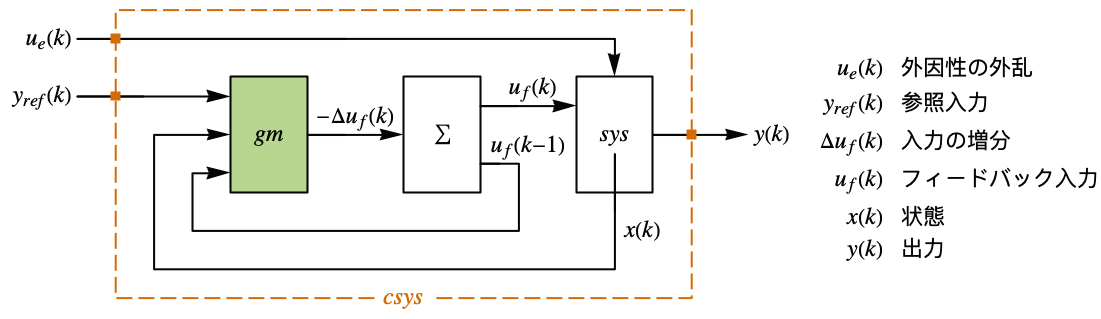
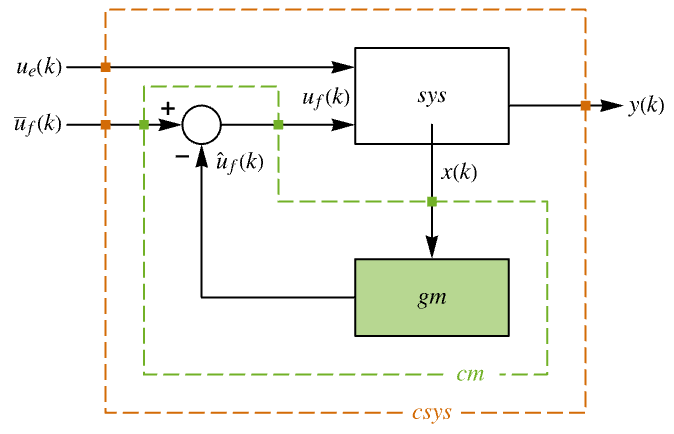
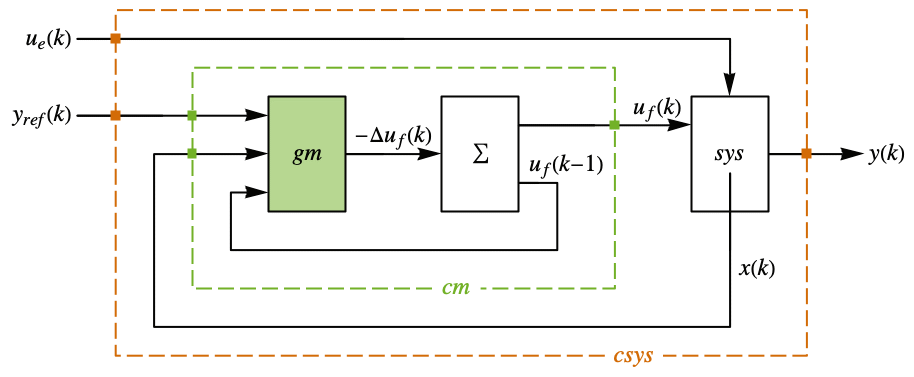
  • 次は，閉ループ系の特性である．
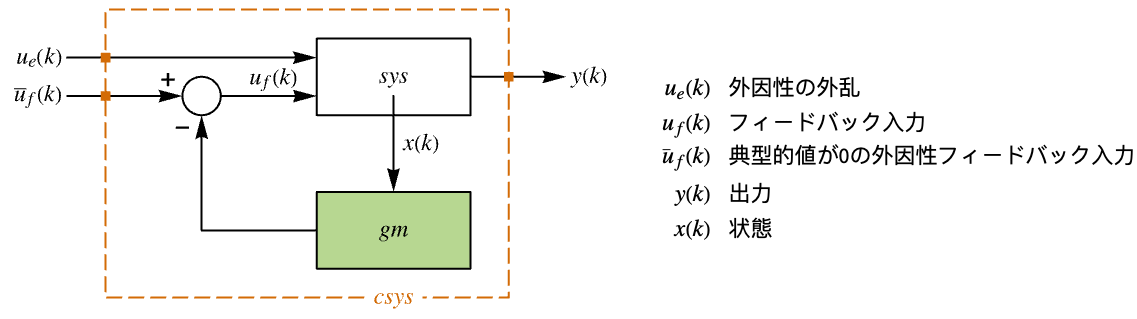
  • "ClosedLoopPoles"線形化された"ClosedLoopSystem"の極
    "ClosedLoopSystem"系 csys
    {"ClosedLoopSystem", cspec}閉ループ系の形式についての詳細制御
    "ControllerModel"モデル cm
    "FeedbackGains"ゲイン行列 κ またはそれと同等のもの
    "FeedbackGainsModel"モデル gm
    "FeedbackRegions"フィードバックがそこから実行可能な領域
    "QuasiClosedLoopSystem""QuasiFeedbackGains"で組み立てられた閉ループ系
    "QuasiFeedbackGains"初期値のみに依存するフィードバックゲイン
    "QuasiFeedbackGainsModel""QuasiFeedbackGains"の系のモデル
    "OptimalCost" 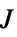の最適値
  • 次は，無限範囲問題の特性である．
  • "MaximalLQRInvariantRegion"LQRフィードバックゲインがある最大領域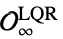
    "MaximalStabilizableRegion"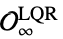に誘導できる最大領域 K_infty TemplateBox[{{(, O}, infty, LQR}, Subsuperscript]
    "MinimalFiniteHorizon"K_infty TemplateBox[{{(, O}, infty, LQR}, Subsuperscript])における状態が 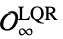に入る最大範囲
  • 次は，基本的な設計特性である．
  • "Design"コントローラ設計のタイプ
    "DesignModel"設計に使用されたモデル
    "DesignModelSamplingMethod""DesignModel"を得るために使われたサンプリングメソッド
    "DesignModelSamplingPeriod""DesignModel"のサンプリング周期
    "Horizon"範囲 η
    "Norm"1-ノルム，平方された2-ノルムあるいは∞-ノルム
  • 次は入力モデルの特性である．
  • "FeedbackInputs"フィードバックに使われる sys の入力 uf
    "InputModel"入力モデル sys
    "InputsCount"sys の入力 u の数
    "OpenLoopPoles""DesignModel"の極
    "OutputsCount"sys の出力 y の数
    "SamplingPeriod"sys のサンプリング周期
    "StatesCount"sys の状態 x の数
    "TrackedOutputs"sys の追跡される出力 yt

    • 次は，標準的レイアウトの線図である．

    次は，追跡レイアウトの線図である．

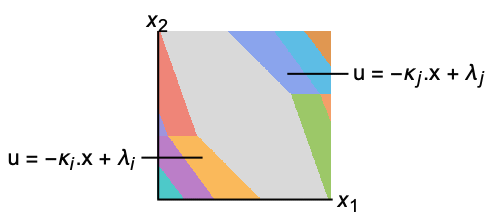
例題

すべて開くすべて閉じる

例  (2)

状態{x1,x2}，制御入力 u の系についての無限範囲の調整器問題を解く：

費用を指定する：

状態と入力の制約条件も指定する：

結果のモデル予測制御コントローラを計算する：

閉ループ系：

実行可能なフィードバックがある領域：

実行可能領域内で初期点を変えた閉ループ系のシミュレーション：

状態が{x1,x2}でコントロール入力が u の系についての有限範囲調整器問題を解く：

費用 を指定する：

状態と入力の制約条件も指定する：

結果のモデル予測制御コントローラを計算する：

閉ループ系：

閉ループ系の入力列に対する応答：

擬似閉ループ系：

擬似閉ループ系の入力列に対する応答：

スコープ  (43)

基本的な用法  (5)

状態{x1,x2}，制御入力 u の離散時間系についての制御器問題を解く：

を最小化する：

状態と制御入力に制限を加える：

コントローラを計算する：

閉ループ系：

閉ループ系の応答：

上記からの閉ループ系：

この系は，入力モデル，フィードバックゲイン，比較器からなる：

部分系の次数：

非零の初期条件で閉ループ系のシミュレーションを行う：

異なる初期条件で開始する：

入力{u1,u2}の多入力系：

費用：

制約条件：

コントローラを計算する：

コントローラはDiscreteInputOutputModelである：

これは基本的に一連の区分関数である：

入力として2つの状態を持つ：

サンプリング周期が0.1の系：

費用：

制約条件：

コントローラを計算する：

出力応答：

サンプリング時点での応答をプロットする：

これを時間の関数としてプロットする：

上記からのコントローラデータオブジェクト：

コントローラモデルと閉ループ系を入手してコントローラ努力を計算する：

入力数列に対する出力応答：

の制御境界に沿ったコントローラ努力：

ノルム  (4)

1ノルムのコストを最小化するコントローラを計算する：

このコントローラはDiscreteInputOutputModelである：

これは，一連の区分関数である：

ノルムの費用を最小化するコントローラを計算する：

このコントローラはDiscreteInputOutputModelである：

これは一連の区分関数である：

平方2ノルム費用を最小化するコントローラを計算する：

このコントローラはDiscreteInputOutputModelである：

これは一連の区分関数である：

無限期間用の平方2ノルム費用を最小化するコントローラを計算する：

このコントローラはNonlinearStateSpaceModelである：

状態変数はない：

入力モデルの状態の区分関数である：

追跡  (4)

状態{x1,x2}，制御入力 u の離散時間系の追跡問題を解く：

費用：

制約条件：

追跡コントローラを計算する：

閉ループ系：

閉ループ応答：

上記からの閉ループ系：

制約条件がない階段状の参照信号に対する応答：

この応答は上限の5を超えない：

正弦波参照に対する応答：

異なるノルムの応答と比較する：

異なるノルムのためのコントローラ：

閉ループ系：

応答：

1ノルムとノルムの応答は，単一入力単一出力の系なので等しい：

2ノルム応答と1ノルム応答の誤差ノルム：

多出力系のノルムと比較する：

異なるノルムの費用指定：

コントローラ：

閉ループ系：

応答：

1ノルム応答とノルム応答の費用の違い：

工場モデル  (8)

StateSpaceModelとして指定された系のコントローラ：

AffineStateSpaceModelとして指定された系：

コントローラ：

これは線形近似に基づいて計算される：

フィードバックゲインは等しい：

非零の操作点がある非線形系：

コントローラ：

これは線形近似に基づいて計算される：

非零の操作点によってゲインが変わってくる：

NonlinearStateSpaceModelとして指定された系のコントローラ：

連続時間SystemModelとして指定された系：

完全な系の指定にはサンプリングも含まれている：

費用：

形式変数によって指定された制約条件：

コントローラ：

制約条件は変数ラベルを使って指定することもできる：

コントローラ：

フィードバックゲインは等しい：

フィードバック入力と外因性入力がある系：

完全な系の指定：

費用にはフィードバック入力の費用だけが含まれる：

制約条件にはフィードバック入力の制約条件だけが含まれる：

コントローラ：

フィードバックゲインモデルには入力としての2つの状態{x1,x2}と出力としての u1がある：

多出力の系：

最初の入力だけを追跡するための完全な系の指定：

費用には追跡された出力の誤差だけが含まれる：

制約条件：

コントローラ：

最初の出力だけが追跡される：

複数の入力があるSystemModel：

変数名を使って指定されたフィードバック入力：

フィードバック入力の指標：

これは線形化されたStateSpaceModelの最初の入力である：

制約条件  (5)

論理式として指定された制約条件：

リストとして指定された制約条件：

ベクトルとスカラーの不等式制約として指定された制約条件：

特定の について指定された制約条件：

制御率を含む制約条件：

コントローラデータを計算する：

閉ループ系の応答：

コントローラ努力：

制御率にはという制限がある：

特性  (17)

使用可能な特性のリストはコントローラのデータオブジェクトから計算できる：

特定の特性は直接計算できる：

特性のリストも計算できる：

フィードバックゲイン：

一連の区分関数である：

状態はアフィンである：

これを使ってフィードバックゲインモデルが計算できる：

フィードバックゲインモデルを直接入手する：

これを使ってコントローラモデルが計算できる：

閉ループ系も計算できる：

最適費用：

3つの区分関数の和である：

各インスタントで最適費用である：

二次でもある：

インスタンスが最小のものから最大のものへとソートする：

各インスタンスの最適費用は区分二次である：

1ノルム問題の最適費用：

各インスタンスの最適費用は区分線形である：

ノルム問題の最適費用：

各インスタンスの最適費用は区分線形である：

範囲問題の最適費用：

これは区分的二次式である：

範囲問題の関心領域：

"MaximalLQRInvariantRegion"は"MaximalStabilizableRegion"内に含まれている：

"MaximalStabilizableRegion"は，基本的に，"FeedbackRegions"と同じである：

"FeedbackRegions"は複数の凸部分領域からなっている：

"MaximalStabilizableRegion"は単一の凸領域である：

範囲問題の閉ループの極は区分関数である：

有限範囲問題の閉ループの極は一連の区分関数である：

擬似フィードバックゲイン：

これらは区分関数である：

系の初期状態にしか依存しない：

擬似フィードバックゲインモデル：

これは擬似フィードバックゲインから計算される：

擬似閉ループ系：

これは擬似フィードバックゲインモデルから計算される：

基本的な設計の特性：

入力モデル特性：

すべての特性をAssociationとして得る：

あるいはDatasetとして得る：

アプリケーション  (2)

患者の薬物動態管理を自動化するコントローラを設計する：»

薬物動態学(PK)特徴のモデル：

薬力学(PD)特徴のモデル：

Hill方程式を使ったバイスペクトラルインデックス(BIS)と の間の関係のモデル：

Hill方程式の非線形の特徴を示すプロット：

が入力，が出力のコンパートメントモデル：

モデルの離散時間近似：

費用を設定して出力を追跡する：

を計算して完全に目覚めており中程度ではあるが深い催眠状態にはないBIS値を求める：

患者が深い催眠状態に陥ることを防ぐための制約条件を指定する：

コントローラを計算する：

閉ループ系：

患者が適度の催眠状態になるBIS値に達する を計算する：

自動過程における プロット：

BISプロット：

等温連続攪拌タンク反応器過程を改善するコントローラを設計する：»

状態，入力の系のモデル：

モデルの離散時間近似を計算する：

開ループ系の応答：

MPCコントローラを設計する：

閉ループ系：

閉ループ系の応答：

開ループ系と閉ループ系の応答を比較する：

コントローラ努力：

特性と関係  (3)

LQRegulatorGainsは平方2ノルム無限範囲問題の特殊ケースである：

制約条件がないModelPredictiveControllerは基本的に同じ結果を与える：

LQRegulatorGainsは制約条件を考慮しない：

ModelPredictiveControllerは状態と制御条件を考慮する：

結果としてLQRegulatorGainsには1セットのフィードバックゲインしかない：

一方，ModelPredictiveControllerのフィードバックゲインは区分関数である：

これはフィードバックが可能な領域も計算する：

実行可能領域の境界を計算する：

LQR閉ループ系のシミュレーションを実行可能領域外の で行う：

制御条件が満たされていない：

実行不可能な初期値 からのMPCコントローラによる閉ループ系の応答：

実行可能な初期値 を使ったLQRとMPCの閉ループ系の応答：

コントローラの応答はLQRコントローラが今回も制御条件を満たしていないことを示している：

MPCコントローラは複数の多重パラメータ最適化問題を解くことで計算される：

二次費用を計算する関数：

制約条件を組み立てる関数：

変数を組み立てる関数：

さまざまな例について最適化問題を解く：

ModelPredictiveControllerは基本的に同じ結果を与える：

考えられる問題  (2)

範囲の1ノルムとノルムがサポートされている：

上記を平方2ノルム問題に変更する：

あるいは有限範囲問題にする：

範囲問題についての制約条件には 項と 項は入れられない：

状態変数と入力変数を使って制約条件を指定する：

あるいは範囲を有限にする：

Wolfram Research (2022), ModelPredictiveController, Wolfram言語関数， https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

テキスト

Wolfram Research (2022), ModelPredictiveController, Wolfram言語関数， https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

CMS

Wolfram Language. 2022. "ModelPredictiveController." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ModelPredictiveController.html.

APA

Wolfram Language. (2022). ModelPredictiveController. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ModelPredictiveController.html

BibTeX

@misc{reference.wolfram_2024_modelpredictivecontroller, author="Wolfram Research", title="{ModelPredictiveController}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ModelPredictiveController.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_modelpredictivecontroller, organization={Wolfram Research}, title={ModelPredictiveController}, year={2022}, url={https://reference.wolfram.com/language/ref/ModelPredictiveController.html}, note=[Accessed: 23-November-2024 ]}