ParametricNDSolve

ParametricNDSolve[eqns,u,{x,xmin,xmax},pars]

finds a numerical solution to the ordinary differential equations eqns for the function u with the independent variable x in the range xmin to xmax with parameters pars.

ParametricNDSolve[eqns,u,{x,xmin,xmax},{y,ymin,ymax},pars]

solves the partial differential equations eqns over a rectangular region.

ParametricNDSolve[eqns,u,{x,y}∈Ω,pars]

solves the partial differential equations eqns over the region Ω.

ParametricNDSolve[eqns,u,{t,tmin,tmax},{x,y}∈Ω,pars]

solves the time-dependent partial differential equations eqns over the region Ω.

ParametricNDSolve[eqns,{u1,u2,…},…]

solves for the functions ui.

Details and Options

  • ParametricNDSolve gives results in terms of ParametricFunction objects.
  • A specification for the parameters pars of {pspec1,pspec2,…} can be used to specify ranges.
  • Possible forms for pspeci are:
  • pp has range Reals or Complexes
    Element[p,Reals]p has range Reals
    Element[p,Complexes]p has range Complexes
    Element[p,{v1,…}]p has discrete range {v1,…}
    {p,pmin,pmax}p has range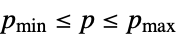
  • In ParametricNDSolve[eqns,{u1,u2,…},…], ui can be any expression. Typically, ui will depend on the parameters indirectly through the solution of the differential equations but may depend explicitly on the parameters. A ParametricFunction object that will return a list can be obtained using ParametricNDSolve[eqns,{{u1,u2,…}},…] or by using ParametricNDSolveValue[eqns,{u1,u2,…},…].
  • Derivatives of the resulting ParametricFunction objects with respect to the parameters are computed using a combination of symbolic and numerical sensitivity methods when possible.
  • ParametricNDSolve takes the same options and settings as NDSolve.
  • NDSolve and ParametricNDSolve typically solve differential equations by going through several different stages, depending on the type of equations. With Method->{s1->m1,s2->m2,…}, stage si is handled by method mi. The actual stages used and their order are determined by NDSolve, based on the problem to be solved.
  • Possible solution stages are the same as for NDSolve, with the addition of:
  • "ParametricCaching"caching of computed solutions
    "ParametricSensitivity"computation of derivatives with respect to parameters

    • List of all options

Examples

open allclose all

Basic Examples  (3)

Get a parametric solution for y:

Evaluating with a numerical value of a gives an approximate function solution for y:

Evaluate at a time :

Plot the solutions for several different values of the parameter:

Get a function of the parameter a that gives the function f at :

This plots the value of f[10] as a function of the parameter a:

Find a value of a for which y[10]=0:

Show the sensitivity of the solution of a differential equation to parameters:

The sensitivity with respect to a increases with t:

The sensitivity with respect to b does not increase with t:

Scope  (5)

Parameter Dependence  (3)

ParametricNDSolve returns a substitution to a ParametricFunction object:

Get the solution for :

Plot the solution for :

Plot solutions for values of ranging from to :

Initial conditions can be specified as parameters:

Plot solutions with with for values of ranging from to :

Plot solutions with with for values of ranging from to :

Differential equation coefficients and boundary conditions can be specified as parameters:

Plot solutions with for values of ranging from to and with and :

Parameter Sensitivity  (2)

Solve the classical harmonic oscillator with parametric amplitude :

Plot the solution for and several nearby values of :

The sensitivity of with respect to is by definition . Plot the sensitivity at :

Plot the sensitivity as a band around the solution for :

Sensitivity analysis of a differential equation with multiple parameters:

Plot the sensitivity with respect to the initial condition at , :

Plot the sensitivity with respect to the initial condition at , :

Generalizations & Extensions  (1)

Solve , for various values of WorkingPrecision and plot the error:

Options  (2)

Method  (2)

ParametricCaching  (1)

Prevent caching of solutions to save memory:

With no caching, the only extra memory required is for the processed equations:

The default is to cache the most recently computed solution:

With caching, the memory requirement is much greater:

ParametricSensitivity  (1)

Specify that no sensitivity should be computed:

The function evaluates quickly:

The derivative is not computed:

Applications  (10)

Parameter Sweeps  (4)

Find an initial value for which the solution of a differential equation will have :

Find a solution with :

Check the resulting solution:

Compare to nearby values of the parameter s:

Find several solutions to the boundary value problem , , . First consider several possible values for :

Run a parameter sweep to determine nontrivial solution values of :

Using approximate initial values from the graph above:

Plot the solutions that were found:

Find all eigenvalues and eigenfunctions for with . Start by exploring the possible parameter values:

Find the exact values for :

Plot them:

Find the value of for which the solution of , has minimal arc length from to . Begin by plotting the solutions for values of ranging from 0 to 1:

Plot versus the arc length of the solution:

The minimum arc length solution for seems to occur at :

Find the local minimum, which appears near :

Plot the corresponding solution of (locally) minimal arc length together with some nearby solutions:

Parameter Sensitivities  (4)

Perturb a parameter in a differential equation and view several of the resulting perturbed solutions:

Plotting the sensitivity solutions gives qualitatively the same result:

Simulate an inverted pendulum stabilized by an oscillating base:

Sensitivity of with respect to the amplitude a increases with time:

Parametric dependence of the heat equation , :

Find the sensitivities and :

Plot the corresponding sensitivity bands:

Indicate sensitivity to a and c by changing the color of the solution surface:

Find the sensitivity of the Lorenz equations to a parameter:

Parameter Fitting  (2)

Sample the solution of a differential equation and add noise:

Fit a trigonometric model to the noisy data:

A quadratic model is a better fit:

Find the parameters that make the solution of a differential equation the best fit to data:

The data comes from a cooling body, so use Newton's law of cooling:

Properties & Relations  (1)

Use SystemModelParametricSimulate to simulate larger hierarchical system models:

Simulate with two sets of resistor and spring damper parameters:

Compare the resulting angular velocities:

Wolfram Research (2012), ParametricNDSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/ParametricNDSolve.html (updated 2014).

Text

Wolfram Research (2012), ParametricNDSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/ParametricNDSolve.html (updated 2014).

CMS

Wolfram Language. 2012. "ParametricNDSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ParametricNDSolve.html.

APA

Wolfram Language. (2012). ParametricNDSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParametricNDSolve.html

BibTeX

@misc{reference.wolfram_2024_parametricndsolve, author="Wolfram Research", title="{ParametricNDSolve}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ParametricNDSolve.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parametricndsolve, organization={Wolfram Research}, title={ParametricNDSolve}, year={2014}, url={https://reference.wolfram.com/language/ref/ParametricNDSolve.html}, note=[Accessed: 17-November-2024 ]}