ParametricNDSolve
ParametricNDSolve[eqns,u,{x,xmin,xmax},pars]
関数 u の常微分方程式 eqns の数値解を,独立変数 x(範囲は xminから xmaxまで),パラメータ pars で求める.
ParametricNDSolve[eqns,u,{x,xmin,xmax},{y,ymin,ymax},pars]
偏微分方程式 eqns を矩形領域上で解く.
ParametricNDSolve[eqns,u,{x,y}∈Ω, pars]
偏微分方程式 eqns を領域Ω上で解く.
ParametricNDSolve[eqns,u,{t,tmin,tmax},{x,y}∈Ω, pars]
時間依存偏微分方程式 eqns を領域Ω上で解く.
ParametricNDSolve[eqns,{u1,u2,…},…]
関数 uiを解く.
詳細とオプション


- ParametricNDSolveは結果をParametricFunctionオブジェクトによって返す.
- {pspec1,pspec2,…}のパラメータ pars の指定を使って範囲を指定することができる.
- pspeciの可能な形式
-
p p の範囲はRealsまたはComplexes Element[p,Reals] p の範囲はReals Element[p,Complexes] p の範囲はComplexes Element[p,{v1,…}] p は離散範囲{v1,…}を持つ {p,pmin,pmax} p の範囲は 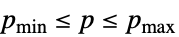 である
である - ParametricNDSolve[eqns,{u1,u2,…},…]では,uiは任意の式でよい.一般に,uiは微分方程式の解を通して間接的にパラメータに依存するが,パラメータに明示的に依存することもある.リストを返すParametricFunctionオブジェクトはParametricNDSolve[eqns,{{u1,u2,…}},…]またはParametricNDSolveValue[eqns,{u1,u2,…},…]を使って得ることができる.
- パラメータについての結果のParametricFunctionオブジェクトの導関数は,可能な場合は数値感度メソッドと記号感度メソッドを組み合せて計算される.
- ParametricNDSolveにはNDSolveと同じオプションと設定が使える.
- NDSolveとParametricNDSolveは,一般に,方程式のタイプによっていくつかの異なる段階に分けて微分方程式を解く.Method->{s1->m1,s2->m2,…}とすると,段階 siがメソッド miで処理される.実際に使われる段階とその順序は,解く問題に基づいてNDSolveによって決定される.
- 可能な解の段階はNDSolveのものに以下を加えたものである.
-
"ParametricCaching" 計算された解をキャッシュする "ParametricSensitivity" パラメータについての導関数の計算
全オプションのリスト

例題
すべて開くすべて閉じる例 (3)
スコープ (5)
パラメータ依存 (3)
ParametricNDSolveはParametricFunctionオブジェクトの代替オブジェクトを返す:
一般化と拡張 (1)
WorkingPrecisionのさまざまな値について ![]() ,
, ![]() を解き,誤差をプロットする:
を解き,誤差をプロットする:
オプション (2)
アプリケーション (10)
特性と関係 (1)
SystemModelParametricSimulateを使って大きい階層的系のモデルのシミュレーションを行う:
テキスト
Wolfram Research (2012), ParametricNDSolve, Wolfram言語関数, https://reference.wolfram.com/language/ref/ParametricNDSolve.html (2014年に更新).
CMS
Wolfram Language. 2012. "ParametricNDSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ParametricNDSolve.html.
APA
Wolfram Language. (2012). ParametricNDSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParametricNDSolve.html