PermutationReplace

PermutationReplace[expr,perm]

expr の各部分を置換 perm におけるその像で置き換える．

PermutationReplace[expr,gr]

置換群 gr のすべての要素における expr の像のリストを返す．

詳細

  • 置換 perm の巡回に存在する expr の整数 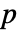については，像は 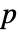の右の整数，あるいは 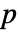が最後である場合には巡回の最初の整数である．perm の巡回に存在しない整数 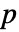については，像は 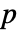自身である．
  • g が expr の置換オブジェクトであるなら，作用は右共役作用PermutationProduct[InversePermutation[perm],g,perm]であると理解される．これは，g の巡回にある点を perm における自身の像で置換することに等しい．
  • 置換群 expr に適用されると，PermutationReplace は個々の生成元に作用し，同じ抽象群を返すが，違った点に作用する．
  • 引数はどちらも個々にリストすることができる．どちらの引数もリストである場合には，第2引数が最初に縫い込まれる．

例題

すべて開くすべて閉じる

例  (2)

Cycles[{{2,3,4,6}}]における整数4の像は，整数6である：

恒等置換では，整数は移動しない：

別の置換に対する置換の作用は，共役作用として理解される：

群の全要素における像：

スコープ  (6)

置換の台における点の像は，点の右隣の点である：

巡回の最後の点の像は，その巡回の最初の点である：

置換の台にない点は不変である：

整数列にPermutationReplaceを使うと，それぞれの像のリストを返す：

別の置換にPermutationReplaceを使うと，共役作用であると理解される：

置換群では，生成元は共役である：

第2引数はリストにすることができる：

どちらの引数もリストである場合には，第2引数が最初に縫い込まれる：

群の全要素における像：

特性と関係  (4)

PermutationReplaceは，PermutationProductについて右作用である：

恒等置換リストに対してPermutationReplaceはPermutationListに一致する：

恒等置換のリストに対するPermutationReplaceはPermuteとは逆の結果を生ずる：

置換群における点の軌道は，群の要素におけるその点の像の和集合である：

おもしろい例題  (1)

像のリストでソートされた群の要素のグラフィカル表記：

Wolfram Research (2010), PermutationReplace, Wolfram言語関数， https://reference.wolfram.com/language/ref/PermutationReplace.html.

テキスト

Wolfram Research (2010), PermutationReplace, Wolfram言語関数， https://reference.wolfram.com/language/ref/PermutationReplace.html.

CMS

Wolfram Language. 2010. "PermutationReplace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationReplace.html.

APA

Wolfram Language. (2010). PermutationReplace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationReplace.html

BibTeX

@misc{reference.wolfram_2024_permutationreplace, author="Wolfram Research", title="{PermutationReplace}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationReplace.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_permutationreplace, organization={Wolfram Research}, title={PermutationReplace}, year={2010}, url={https://reference.wolfram.com/language/ref/PermutationReplace.html}, note=[Accessed: 17-November-2024 ]}