Piecewise

Piecewise[{{val1,cond1},{val2,cond2},…}]

制約条件 condiによって定義された区域の値 valiを持つ区分関数を表す．

Piecewise[{{val1,cond1},…},val]

condiがどれもあてはまらない場合はデフォルト値 val を使う．val のデフォルト値は0である．

詳細

  • condiは一般に 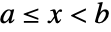のような不等式である．
  • condiは，そのうちのどれかがTrueを返すまで順繰りに評価される．
  • 先行するすべての condiがFalseを返した場合は，Trueを返した最初の condiに対応する valiが区分関数の値として返される．
  • 先行する condiのいずれかが実質的にFalseを返さなかった場合，Piecewise関数は記号的に返される．
  • 返された形式に明示的に含まれている valiのみが評価される．
  • {vali,False}という形式の要素は，最初の{vali,True}の後のすべての要素と同様に削除される．
  • Piecewise[conds]を評価すると自動的にPiecewise[conds,0]になる．
  • PiecewiseはIntegrate，Minimize，Reduce，DSolve，Simplifyのような関数およびその数値バージョンで使うことができる．
  • Piecewise[{{v1,c1},{v2,c2},…}]は
    v1c1
    v2c2
    …
    という形で入力することができる．区分演算子はpwまたは\[Piecewise]として入力できる．値と条件のグリッドは，まずと入力し，続いて とを使って作ることができる．
  • StandardFormとTraditionalFormでは，Piecewise[{{v1,c1},{v2,c2},…}]は通常
    v1c1
    v2c2
    …
    におけるようにカッコを使って出力される．

例題

すべて開くすべて閉じる

例  (3)

零より大きい部分と零より小さい部分で区分が異なる区分関数を設定する：

区分関数の導関数を求める：

pwでを，とTemplateBox[{ctrl, return}, Key1, BaseStyle -> {ExampleText, FontWeight -> Plain, FontFamily -> Source Sans Pro}]で追加的な区分を入力する：

スコープ  (12)

区分関数を定義する：

特定の点でこの関数を評価する：

これをプロットする：

仮定の下で，これを精緻化する：

Piecewise関数の自動簡約：

達成不可能な場合を削除する：

Falseの条件を削除する：

同じ値の場合を一緒にする：

範囲内の値が指定されていない場合，その値は零であるとされる：

次は，デフォルト値を1と指定する：

区分関数の極限を計算する：

正の虚軸の方向に極限を計算する：

区分関数の級数を計算する：

区分関数を積分する：

積分定数は結果が連続的になるように選ばれる：

区分関数の定積分を計算する：

区分関数のラプラス(Laplace)変換：

区分微分方程式を解く：

区分方程式を簡約する：

陰的な区分被積分関数の積分がPiecewiseの明示的な結果を与えることがある：

記号的最小化が区分関数を与えることがある：

アプリケーション  (1)

楕円の体積を計算する：

特性と関係  (11)

PiecewiseExpandはネストした区分関数を単一の区分関数に変換する：

Min，Max，UnitStep，Clipは実引数を取る区分関数である：

Abs，Sign，Argは，引数が実数であると仮定される場合は区分関数である：

KroneckerDeltaとDiscreteDeltaは，複素引数を持つ区分関数である：

Booleはブール引数の区分関数である：

If，Which，Switchは区分関数であると解釈できる：

Floor，Ceiling，Round，IntegerPart，FractionalPartを有限範囲について変換する：

場合数が有限のとき，ModとQuotientを変換する：

UnitBoxとUnitTriangleは実引数の区分関数である：

SquareWave，TriangleWave，SawtoothWaveを有限範囲で変換する：

BernsteinBasisとBSplineBasisは実引数の区分関数である：

考えられる問題  (1)

関数が実変数で一変量でない限り，導関数は区間ごとに計算される：

が実数であるとの指定には，第1条件に不等式を使う：

この関数は で不連続である：

Wolfram Research (2004), Piecewise, Wolfram言語関数， https://reference.wolfram.com/language/ref/Piecewise.html （2008年に更新）.

テキスト

Wolfram Research (2004), Piecewise, Wolfram言語関数， https://reference.wolfram.com/language/ref/Piecewise.html （2008年に更新）.

CMS

Wolfram Language. 2004. "Piecewise." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Piecewise.html.

APA

Wolfram Language. (2004). Piecewise. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Piecewise.html

BibTeX

@misc{reference.wolfram_2024_piecewise, author="Wolfram Research", title="{Piecewise}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Piecewise.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_piecewise, organization={Wolfram Research}, title={Piecewise}, year={2008}, url={https://reference.wolfram.com/language/ref/Piecewise.html}, note=[Accessed: 23-November-2024 ]}