Piecewise

Piecewise[{{val1,cond1},{val2,cond2},…}]

表示一个分段函数，在定义域内的条件 condi 值为 vali.

Piecewise[{{val1,cond1},…},val]

如果没有条件 condi，则取默认值 val. val 的默认值是 0.

更多信息

  • condi 通常是不等式，比如 .
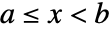  • 依次判断条件 condi，直到其中的一个条件为 True.
  • 如果前面提到的所有条件 condi 都为 False，则把与第一个为 True 的条件 condi 相对应的值 vali，作为分段函数的函数值返回.
  • 如果前面所提到的任意一个条件 condi 不为 False，则分段函数 Piecewise 将会获得符号形式的值.
  • 仅仅对那些直接包括在返回值列表中的参数 vali 进行条件判断.
  • {vali,False} 形式的元素将会被舍弃. 在第一个 {vali,True} 形式之后的所有元素也会被舍弃.
  • Piecewise[conds] 自动计算 Piecewise[conds,0].
  • Piecewise 可以用在 Integrate、Minimize、Reduce、DSolve 和 Simplify 这样的函数中，包括它们的数字形式.
  • Piecewise[{{v1,c1},{v2,c2},…}] 可以按照
    v1c1
    v2c2
    …
     的形式输出. 分段操作符 可以作为 pw 或者 \[Piecewise] 进行输入. 通过第一次输入 、然后用 和 ，可以构造参数值和条件数之间的网格结构.
  • 在 StandardForm 和 TraditionalForm 中，Piecewise[{{v1,c1},{v2,c2},…}] 通常用大括号进行输出，如
    v1c1
    v2c2
    …
    .

范例

打开所有单元关闭所有单元

基本范例  (3)

构造一个有不同的小于零和大于零的分段的分段函数：

获得分段函数的导数：

利用 pw 来输入 ，然后是 ，接着使用 TemplateBox[{ctrl, return}, Key1, BaseStyle -> {ExampleText, FontWeight -> Plain, FontFamily -> Source Sans Pro}] 输入其他分支情况：

范围  (12)

定义一个分段函数：

求出分段函数在具体点上的值：

绘制分段函数的图形：

在假设条件下重新定义函数：

自动化简函数 Piecewise：

去掉取不到值的情况；

去掉 False 条件：

合并含有相同参数值的情况：

如果参数值在一个区域内没有指定，则假设为零：

这里指定默认的参数值应该为 1：

计算分段函数的极限：

计算分段函数在正虚轴方向上的极限：

计算分段函数的级数：

求出分段函数的积分：

选择积分常量，使得输出结果是连续的：

计算分段函数的定积分：

分段函数的拉普拉斯变换：

求解分段的微分方程：

化简分段方程式：

求分段的隐式函数的积分，可以得到直接的 Piecewise 结果：

符号最简化可以得出分段函数：

应用  (1)

计算出椭圆体的体积：

属性和关系  (11)

PiecewiseExpand 把嵌套的分段函数转化为简单的分段函数：

Min、Max、UnitStep 和 Clip 都是带有实参的分段函数：

Abs、Sign 和 Arg 在参数假设为真值的情况下是分段函数：

KroneckerDelta 和 DiscreteDelta 是复数变量的分段函数：

Boole 是布尔参数的分段函数：

If、Which 和 Switch 可以被看成是分段函数：

把 Floor、Ceiling、Round、IntegerPart 和 FractionalPart 转化到有限域中：

当分段数为有限值时，转化 Mod 和 Quotient：

UnitBox 和 UnitTriangle 是含有实参的分段函数：

在有限范围内转换 SquareWave， TriangleWave 和 SawtoothWave ：

BernsteinBasis 和 BSplineBasis 是含有实参的分段函数：

可能存在的问题  (1)

除非函数是单变量函数并且自变量是实数，否则导数将被分段计算：

在第一个条件里使用不等式来指定 为实数：

函数在 处不连续：

Wolfram Research (2004)，Piecewise，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Piecewise.html （更新于 2008 年）.

文本

Wolfram Research (2004)，Piecewise，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Piecewise.html （更新于 2008 年）.

CMS

Wolfram 语言. 2004. "Piecewise." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2008. https://reference.wolfram.com/language/ref/Piecewise.html.

APA

Wolfram 语言. (2004). Piecewise. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Piecewise.html 年

BibTeX

@misc{reference.wolfram_2024_piecewise, author="Wolfram Research", title="{Piecewise}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Piecewise.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_piecewise, organization={Wolfram Research}, title={Piecewise}, year={2008}, url={https://reference.wolfram.com/language/ref/Piecewise.html}, note=[Accessed: 23-November-2024 ]}