PossibleZeroQ
PossibleZeroQ[expr]
gives True if basic symbolic and numerical methods suggest that expr has value zero, and gives False otherwise.
Details and Options
- The general problem of determining whether an expression has value zero is undecidable; PossibleZeroQ provides a quick but not always accurate test.
- With the setting Method->"ExactAlgebraics", PossibleZeroQ will use exact guaranteed methods in the case of explicit algebraic numbers.
Examples
open allclose allBasic Examples (1)
Scope (4)
Options (2)
Assumptions (1)
For arbitrary complex x, f is not identically zero:
When Re[x]>0, f is identically zero:
Method (1)
By default, numeric approximations may be used to decide that an algebraic number is zero:
Approximate methods may give incorrect positive answers:
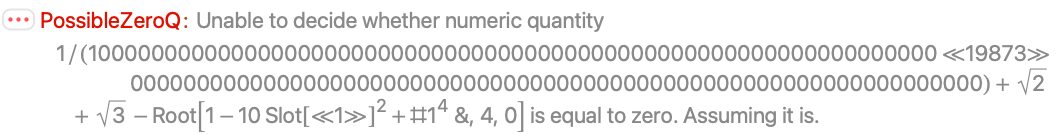
With Method->"ExactAlgebraics" exact methods are used for explicit algebraic numbers:
For explicit algebraic numbers the answer is provably correct:
Applications (1)
Properties & Relations (1)
SameQ[e,0] returns True only if e is explicitly identical to zero:
Equal[e,0] uses simple tests to decide whether e is zero:
When Equal cannot decide whether an expression is zero it returns unchanged:
PossibleZeroQ uses numeric methods to test whether ee is zero:
FullSimplify proves symbolically that ee is zero:
Possible Issues (1)
PossibleZeroQ may return True for nonzero numeric expressions that are close to zero:
Text
Wolfram Research (2007), PossibleZeroQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PossibleZeroQ.html.
CMS
Wolfram Language. 2007. "PossibleZeroQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PossibleZeroQ.html.
APA
Wolfram Language. (2007). PossibleZeroQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PossibleZeroQ.html