RecurrenceTable

RecurrenceTable[eqns,expr,{n,nmax}]

generates a list of values of expr for successive n based on solving the recurrence equations eqns.

RecurrenceTable[eqns,expr,nspec]

generates a list of values of expr over the range of n values specified by nspec.

RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]

generates an array of values of expr for successive n1, n2, … .

Details and Options

  • The eqns must be recurrence equations whose solutions over the range specified can be determined completely from the initial or boundary values given.
  • The eqns can involve objects of the form a[n+i] where i is any fixed integer.
  • The range specification nspec can have any of the forms used in Table.
  • The following options can be given:
  • DependentVariables Automaticthe list of all dependent variables
    Method Automaticmethod to use
    WorkingPrecision Automaticprecision used in internal computations
  • With DependentVariables->Automatic, RecurrenceTable attempts to determine the dependent variables by analyzing the equations given.
  • With WorkingPrecision->Automatic, results for exact inputs are computed exactly, and for inexact inputs, the precision to use is determined adaptively at each iteration.
  • With WorkingPrecision->p, a fixed precision p is used for all iterations.

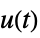
Examples

open allclose all

Basic Examples  (4)

Solve an initial-value problem for a first-order difference equation:

Find the first few Fibonacci numbers:

Study the evolution for a nonlinear map of the plane:

Compute a table of Stirling numbers of the first kind:

Scope  (9)

Ordinary Difference Equations  (6)

Linear ordinary difference equation with exact coefficients:

Nonlinear ordinary difference equation with inexact coefficients:

System of ordinary difference equation with symbolic initial conditions:

Return only the values of x:

Iterate using exact arithmetic:

Iterate using adaptive arithmetic starting with precision 20:

The precision decreases with each iteration:

Iterate using fixed 20-digit-precision arithmetic:

Iterate using machine arithmetic:

Iterate several values at once by giving a vector initial condition:

Iterate a matrix recurrence:

Partial Difference Equations  (2)

Use the partial recurrence equations for binomial coefficients:

Procedural solution for a nonlinear partial difference equation:

Difference-Algebraic Equations  (1)

Solve a linear difference-algebraic equation with constant coefficients:

Compare with the symbolic solution given by RSolve:

Generalizations & Extensions  (3)

Generate a subset of values from a given range:

Get only the last value from an iteration:

This is faster than when all the values are saved:

Use a vector initial condition:

Options  (3)

DependentVariables  (1)

Use DependentVariables to specify the variables when you only want to save some of them:

Save only y:

Save both in order {y,x}:

Method  (1)

Use Method->{Compiled->False} to prevent the Wolfram Language compiler from being used:

Results differ due to arithmetic change from optimization:

WorkingPrecision  (1)

Use WorkingPrecision->MachinePrecision for the fastest iterations:

Use WorkingPrecision->p for slower, but higher-precision iterations:

Exact computations have no error, but may be very slow indeed:

Applications  (6)

Logistic Equations  (1)

Study the behavior of the logistic equation for different values of the parameter r:

Random Number Generation  (1)

Implement the Cliff random number generator:

The random numbers appear to be uniformly distributed:

Compare with the parameters for the uniform distribution:

Rabbit Fractal  (1)

Plot the Douady rabbit fractal:

Initial condition with 250 points in each direction on the rectangle with corners -1.3-1.3 ⅈ and 1.3+1.3 ⅈ:

Iterate starting from these initial conditions:

Use ArrayPlot to show the fractal:

Bifurcation Diagram of the Logistic Map  (1)

Find iterates from and of the map for 1000 values of :

Scale the iterates to be integers between 1 and and transpose so the rows correspond to :

Define a function that gives a rule based on the logarithm of counts of each value:

Make a sparse matrix based on applying Count to the iterates for each :

Use ArrayPlot to make the bifurcation diagram:

Compare Numerical Methods for ODEs  (1)

For , Euler's method is unconditionally unstable:

The symplectic Euler method is stable, but is very sensitive to initial conditions for large h:

Compare the methods for different vector fields with Manipulate:

Standard Map  (1)

Stretching and folding induced by the standard map for a line of initial conditions [more info]:

Properties & Relations  (2)

RSolve finds a symbolic solution for this difference equation:

RecurrenceTable generates a procedural solution for the same problem:

Use RecurrenceFilter to filter a signal:

Obtain the same result using RecurrenceTable:

Neat Examples  (1)

Visualize the smoothing of the initial data for the heat equation using the discretized version:

Wolfram Research (2008), RecurrenceTable, Wolfram Language function, https://reference.wolfram.com/language/ref/RecurrenceTable.html.

Text

Wolfram Research (2008), RecurrenceTable, Wolfram Language function, https://reference.wolfram.com/language/ref/RecurrenceTable.html.

CMS

Wolfram Language. 2008. "RecurrenceTable." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RecurrenceTable.html.

APA

Wolfram Language. (2008). RecurrenceTable. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RecurrenceTable.html

BibTeX

@misc{reference.wolfram_2023_recurrencetable, author="Wolfram Research", title="{RecurrenceTable}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/RecurrenceTable.html}", note=[Accessed: 08-December-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_recurrencetable, organization={Wolfram Research}, title={RecurrenceTable}, year={2008}, url={https://reference.wolfram.com/language/ref/RecurrenceTable.html}, note=[Accessed: 08-December-2023 ]}