WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

TensorWedge[tensor1,tensor2,…]

tensoriの反対称化されたテンソル積を表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
特性と関係  
考えられる問題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

TensorWedge

TensorWedge[tensor1,tensor2,…]

tensoriの反対称化されたテンソル積を表す．

詳細

  • TensorWedge[a,b]は ab として入力できる．記号 は t^ あるいは\[TensorWedge]として入力する．
  • 明示的配列あるいは記号配列のテンソルくさび積では，配列によって階数は異なるかもしれないが，すべてのスロットが同じ次元 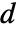でなければならない．TensorWedgeはCrossを一般化する．それには長さ 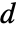の 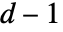個のベクトルが必要である．
  • 複数の配列のTensorWedge積は反対称配列で，常にSymmetrizedArray形式で与えられる．
  • テンソル tensoriが反対称ではない場合は，積を行う前に事実上反対称にされる．ベクトルは階数1の反対称テンソルであるとみなされる．スカラーは階数0の反対称テンソルであるとみなされる．
  • 反対称テンソル tiのくさび積TensorWedge[t1,…,tk]はMultinomial[r1,…,rk]*Symmetrize[TensorProduct[t1,…,tk],Antisymmetric[All]]と等しい．ただし，riは tiのテンソル階数である．

例題

すべて開く すべて閉じる

例  (1)

明示的なベクトルの反対称化されたテンソル積：

Wolfram Language code: {a, b, c}{x, y, z}

正規形：

Wolfram Language code: Normal[%]

スコープ  (3)

ベクトルのくさび積：

Wolfram Language code: v = {a, b, c, d}; w = {x, y, z, t};
Wolfram Language code: vw
Wolfram Language code: %//SymmetrizedArrayRules

反対称配列のくさび積：

Wolfram Language code: SeedRandom[0]; A = SymmetrizedArray[_ :> RandomInteger[100], {5, 5}, Antisymmetric[All]]; B = SymmetrizedArray[_ :> RandomInteger[100], {5, 5}, Antisymmetric[All]];
Wolfram Language code: AB
Wolfram Language code: %//SymmetrizedArrayRules

記号配列のくさび積：

Wolfram Language code: $Assumptions = { A∈Arrays[{5, 5, 5}, Reals, Antisymmetric[{1, 2, 3}]], B∈Arrays[{5, 5}, Reals, Antisymmetric[{1, 2}]] };
Wolfram Language code: AB + BA//TensorReduce

特性と関係  (11)

くさび積はベクトルについては非可換である：

Wolfram Language code: V = Array[v, 5] W = Array[w, 5]
Wolfram Language code: VW === -WV

くさび積は行列については可換である：

Wolfram Language code: M = Array[m, {5, 5}]; Q = Array[q, {5, 5}];
Wolfram Language code: MQ === QM

結果は常に反対称である：

Wolfram Language code: TensorSymmetry[MQ]

くさび積は結合可能である：

Wolfram Language code: A1 = SymmetrizedArray[_ :> RandomInteger[100], {8, 8}, Antisymmetric[All]]; A2 = SymmetrizedArray[_ :> RandomInteger[100], {8}, Antisymmetric[All]]; A3 = SymmetrizedArray[_ :> RandomInteger[100], {8, 8, 8}, Antisymmetric[All]];
Wolfram Language code: (A1A2)A3 === A1(A2A3) === A1A2A3

単一配列のテンソルくさび積はその反対称化に等しい：

Wolfram Language code: A = Array[Subscript[a, ##]&, {3, 3}]
Wolfram Language code: TensorWedge[A]
Wolfram Language code: % === Symmetrize[A, Antisymmetric[All]]

次元 における 個のベクトルのくさび積のホッジ(Hodge)双対はそれらのベクトルの外積に一致する：

Wolfram Language code: v1 = {a, b, c}; v2 = {x, y, z};
Wolfram Language code: Normal@HodgeDual[v1v2] === Cross[v1, v2]
Wolfram Language code: v1 = {a, b, c, d}; v2 = {x, y, z, t}; v3 = {p, q, r, s};
Wolfram Language code: Normal@HodgeDual[v1v2v3] === Cross[v1, v2, v3]

くさび積ではすべての引数が同じ次元のスロットを持たなければならないが，階数は任意でよい：

Wolfram Language code: a1 = Array[x, {5, 5}]; a2 = Array[y, {5, 5}]; result = a1a2;
Wolfram Language code: TensorDimensions[result]

結果は常に反対称である：

Wolfram Language code: TensorSymmetry[result]

次元 ，ここでは の2つの配列を取る：

Wolfram Language code: a1 = Array[x, {3, 3}]; a2 = Array[y, {3, 3}];

くさび積の総階数が次元 より大きい場合，その積は0である：

Wolfram Language code: a1a2
Wolfram Language code: SparseArray[%]

奇階数の配列とそれ自身とのくさび積は0である：

Wolfram Language code: a = Array[Subscript[x, ##]&, {7, 7, 7}];
Wolfram Language code: aa//SparseArray

しかし，偶階数の場合は結果はゼロ配列ではない：

Wolfram Language code: a = Array[Subscript[x, ##]&, {5, 5}];
Wolfram Language code: aa
Wolfram Language code: SymmetrizedArrayRules[%]

記号配列で：

Wolfram Language code: $Assumptions = { A∈Arrays[{7, 7, 7}, Reals, Antisymmetric[All]], B∈Arrays[{7, 7}, Reals, Antisymmetric[All]] };
Wolfram Language code: AA
Wolfram Language code: BB

くさび積はテンソル積の反対称化に比例する：

Wolfram Language code: V = Array[Subscript[v, #]&, {4}] M = Array[Subscript[m, ##]&, {4, 4}]
Wolfram Language code: VM - 3Symmetrize[VM, Antisymmetric[All]]//Simplify
Wolfram Language code: SparseArray[%]

比例因子は階数のMultinomialである：

Wolfram Language code: Multinomial[1, 2]

長さ の 個のベクトルについて，そのTensorWedgeの唯一の独立成分はそれらのベクトルのリストの行列式に等しい：

Wolfram Language code: v1 = {v11, v12, v13}; v2 = {v21, v22, v23}; v3 = {v31, v32, v33};
Wolfram Language code: TensorWedge[v1, v2, v3][[1, 2, 3]]
Wolfram Language code: % === Det[{v1, v2, v3}]

テンソルくさび積はすべての引数において線形である：

Wolfram Language code: $Assumptions = (A | B)∈Arrays[{8, 8, 8}, Reals, Antisymmetric[All]];
Wolfram Language code: (a A + b B)(c A + d B)//TensorExpand

考えられる問題  (1)

TensorWedgeには属性OneIdentityがある．しかし，TensorWedge[t]は反対称テンソル t についてのみ t と等価である：

Wolfram Language code: TensorWedge[t]
Wolfram Language code: Assuming[t∈Arrays[{d, d, d, d}, Reals, Antisymmetric[{1, 2, 3, 4}]], TensorWedge[t]]

いくつかのスロットのみでの反対称性では十分ではない：

Wolfram Language code: Assuming[t∈Arrays[{d, d, d, d}, Reals, Antisymmetric[{1, 2}]], TensorWedge[t]]
Wolfram Research (2012), TensorWedge, Wolfram言語関数， https://reference.wolfram.com/language/ref/TensorWedge.html.

テキスト

Wolfram Research (2012), TensorWedge, Wolfram言語関数， https://reference.wolfram.com/language/ref/TensorWedge.html.

CMS

Wolfram Language. 2012. "TensorWedge." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TensorWedge.html.

APA

Wolfram Language. (2012). TensorWedge. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TensorWedge.html

BibTeX

@misc{reference.wolfram_2026_tensorwedge, author="Wolfram Research", title="{TensorWedge}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/TensorWedge.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_tensorwedge, organization={Wolfram Research}, title={TensorWedge}, year={2012}, url={https://reference.wolfram.com/language/ref/TensorWedge.html}, note=[Accessed: 02-November-2026]}