TensorWedge

TensorWedge[tensor1,tensor2,…]

表示 tensori 的反对成张量积.

更多信息

  • TensorWedge[a,b] 可以按 ab 输入. 字符 的输入方式为 t^ 或者 \[TensorWedge].
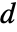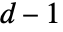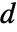  • 在显式或者符号式数组的张量楔积中，所有插槽 (slot) 必须具有相同的维度 ，虽然不同数组可能有不同的阶数. TensorWedge 推广了 Cross，后者需要 个长度为 的向量.
  • 几个数组的 TensorWedge 积是一个反对称数组，总是以 SymmetrizedArray 形式给出.
  • 如果张量 tensori 不是反对称的，那么实际上它们在乘积之前会被反对称化. 向量被视为阶数为1的反对称张量. 标量被视为阶数为0的反对称张量.
  • 反对称张量 ti 的楔积 TensorWedge[t1,…,tk] 等价于 Multinomial[r1,…,rk]*Symmetrize[TensorProduct[t1,…,tk],Antisymmetric[All]]，其中，ri 是 ti 的张量阶数.

范例

打开所有单元关闭所有单元

基本范例  (1)

显式向量的反对称张量积：

规范形式：

范围  (3)

向量的楔积：

反对称数组的楔积：

符号式数组的楔积：

属性和关系  (11)

楔积对向量而言是反交换的：

楔积对矩阵而言是可交换的：

结果总是反对称的：

楔积是可结合的：

单个数组的张量楔积等价于它的反对称版本：

维度 中 个向量的楔积的霍奇对偶与这些向量的叉积一致：

楔积要求所有变量的插槽 (slot) 有相同维度，但是阶数可以是任意的：

结果总是反对称的：

采用维度 中的两个数值，假设 ：

如果楔积的总阶数大于维度 ，那么乘积为0：

阶数为奇数的数组与自身的楔积是零：

但是如果阶数是偶数，那么结果是非零数组：

在符号式数组下：

楔积与张量乘积的反对称性成正比：

比例因子是阶数的 Multinomial：

对于 个长度为 的向量，TensorWedge 的唯一独立分量等于这些向量的列表的判别式：

在所有变量中张量楔积是线性的：

可能存在的问题  (1)

TensorWedge 具有属性 OneIdentity. 但是，TensorWedge[t] 只对于反对称张量 t 才等价于 t：

只在一些插槽 (slot) 进行反对称处理是不够的：

Wolfram Research (2012)，TensorWedge，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorWedge.html.

文本

Wolfram Research (2012)，TensorWedge，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TensorWedge.html.

CMS

Wolfram 语言. 2012. "TensorWedge." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TensorWedge.html.

APA

Wolfram 语言. (2012). TensorWedge. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TensorWedge.html 年

BibTeX

@misc{reference.wolfram_2024_tensorwedge, author="Wolfram Research", title="{TensorWedge}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/TensorWedge.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tensorwedge, organization={Wolfram Research}, title={TensorWedge}, year={2012}, url={https://reference.wolfram.com/language/ref/TensorWedge.html}, note=[Accessed: 21-November-2024 ]}