VectorGreater 
xy 或 VectorGreater[{x,y}]
对于长度为 n 的向量,如果对于所有 ![]() 的元素 xi>yi 成立,则给出 True.
的元素 xi>yi 成立,则给出 True.
xκy 或 VectorGreater[{x,y},κ]
对于 x 和 y,如果 ![]() ,则给出 True,其中 κ 为正常凸锥.
,则给出 True,其中 κ 为正常凸锥.
更多信息


- VectorGreater 给出向量、矩阵和数组的偏序,与向量空间运算兼容,因而对于所有的
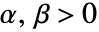 ,
,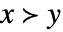 和
和 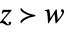 即意味着
即意味着 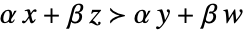 .
. - VectorGreater 通常用于指定约束优化、不等式求解和积分的向量不等式.
- 当 x 和 y 为
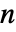 -向量时,xy 等价于
-向量时,xy 等价于  . 即为了使关系式成立,x 的每个元素都大于 y 的相应元素.
. 即为了使关系式成立,x 的每个元素都大于 y 的相应元素. - 当 x 和 y 是维数为
 的数组时,xy 等价于
的数组时,xy 等价于 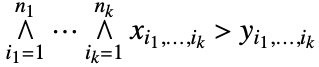 . 即为了使关系式成立,x 的每个元素都大于 y 的相应元素.
. 即为了使关系式成立,x 的每个元素都大于 y 的相应元素. - 如果 x 或 y 有非数字元素,xy 不会进行计算;否则通常会给出 True 或 False.
- x 是长度为 n 的向量,y 为标量时,如果对于所有
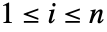 的元素 xi>y 成立,xy 给出 True.
的元素 xi>y 成立,xy 给出 True. - 通过使用字符 (用
 v>
v> 或 \[VectorGreater] 输入),可用以下方式输入带有下标的向量不等式:
或 \[VectorGreater] 输入),可用以下方式输入带有下标的向量不等式: -
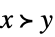
VectorGreater[{x,y}] 标准向量不等式 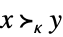
VectorGreater[{x,y},κ] 由锥 κ 定义的向量不等式 - 一般情况下,可以用合适的凸锥 κ 指定向量不等式. 集合
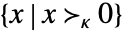 与 κ 相同.
与 κ 相同. - 对于向量 x,
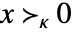 中可能的锥规范 κ 包括:
中可能的锥规范 κ 包括: -
{"NonNegativeCone", n} ![TemplateBox[{n}, NonNegativeConeList] TemplateBox[{n}, NonNegativeConeList]](Files/VectorGreater.zh/22.png)
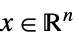 中使得
中使得 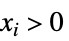 的元素
的元素{"NormCone", n} ![TemplateBox[{n}, NormConeList] TemplateBox[{n}, NormConeList]](Files/VectorGreater.zh/25.png)
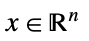 中使得 Norm[{x1,…,xn-1}]<xn 的元素
中使得 Norm[{x1,…,xn-1}]<xn 的元素"ExponentialCone" ![TemplateBox[{}, ExponentialConeString] TemplateBox[{}, ExponentialConeString]](Files/VectorGreater.zh/27.png)
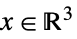 中使得
中使得 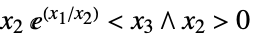 的元素
的元素"DualExponentialCone" ![TemplateBox[{}, DualExponentialConeString] TemplateBox[{}, DualExponentialConeString]](Files/VectorGreater.zh/30.png)
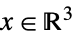 中使得
中使得 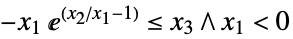 的元素
的元素{"PowerCone",α} ![TemplateBox[{alpha}, PowerConeList] TemplateBox[{alpha}, PowerConeList]](Files/VectorGreater.zh/33.png)
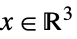 中使得
中使得 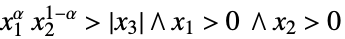 的元素
的元素{"DualPowerCone",α} ![TemplateBox[{alpha}, DualPowerConeList] TemplateBox[{alpha}, DualPowerConeList]](Files/VectorGreater.zh/36.png)
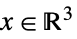 中使得
中使得 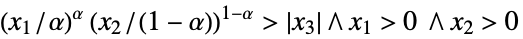 的元素
的元素 - 对于矩阵 x,
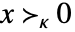 中可能的锥规范 κ 包括:
中可能的锥规范 κ 包括: -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorGreater.zh/40.png)
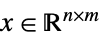 中使得
中使得 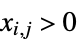 的元素
的元素{"SemidefiniteCone", n} ![TemplateBox[{n}, SemidefiniteConeList] TemplateBox[{n}, SemidefiniteConeList]](Files/VectorGreater.zh/43.png)
对称正定矩阵 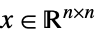
- 对于数组 x,
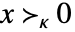 中可能的锥规范 κ 包括:
中可能的锥规范 κ 包括: -
"NonNegativeCone" ![TemplateBox[{}, NonNegativeConeString] TemplateBox[{}, NonNegativeConeString]](Files/VectorGreater.zh/46.png)
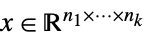 中使得
中使得 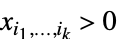 的元素
的元素 - 对于精确数量,VectorGreater 在内部使用数值近似对数字进行排序. 此过程可能被全局变量 $MaxExtraPrecision 的设置所影响.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (7)
表示条件 Norm[{x,y}]<=1:
应用 (1)
VectorGreater 是比较许多元素大小的捷径:
属性和关系 (3)
VectorGreater 与向量空间运算兼容:
Wolfram Research (2019),VectorGreater,Wolfram 语言函数,https://reference.wolfram.com/language/ref/VectorGreater.html.
文本
Wolfram Research (2019),VectorGreater,Wolfram 语言函数,https://reference.wolfram.com/language/ref/VectorGreater.html.
CMS
Wolfram 语言. 2019. "VectorGreater." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/VectorGreater.html.
APA
Wolfram 语言. (2019). VectorGreater. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VectorGreater.html 年