WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

WaveletThreshold

WaveletThreshold[dwd]

DiscreteWaveletDataオブジェクト dwd 中のウェーブレット詳細化係数を閾値化する．

WaveletThreshold[dwd,tspec]

閾値指定 tspec を使って係数を閾値化する．

WaveletThreshold[dwd,tspec,wind]

ウェーブレット指標 wind で与えられるウェーブレット係数を閾値化する．

詳細

WaveletThreshold[dwd]は事実上WaveletThreshold[dwd,"Universal"]である．
WaveletThreshold[dwd,tspec,wind]は，DiscreteWaveletDataで説明されているのと同じ指標の慣習を使ってどの係数を閾値化するかを示す．
デフォルトで，閾値化はすべての細分化レベルで詳細化係数に対して行われる．
閾値指定 tspec の形式は tfun, {tfun,pars}であってもよい．
tfun の使用可能な名前およびオプション

	{"Hard",δ}
	{"Soft",δ}
	{"Firm",δ,r,p}
	{"PiecewiseGarrote",δ}	$0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta$
	{"SmoothGarrote",δ,n}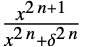
	{"Hyperbola",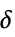}	$ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;$
	{"LargestCoefficients",k}	最も大きい k 個の係数を保存する

すべての場合で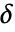，は正の数か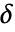，を計算する閾値関数 tfunc とみなされる．各 tfunc[coef_i,wind_i]は正の数を返す．
"Firm"に対する母数の条件は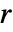，が正の実数であり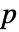が0から1までの正の実数であるというものである．
"SmoothGarrotte"に対する母数の条件は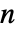，が正の実数であるというものである．
閾値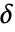は以下の方法で自動的に計算される．

	Automatic	"Universal"閾値化値
	{"FDR",α}	有意水準 α におけるFDR (false discovery rate)
	"GCV"	一般化されたクロス証明関数を最小化する
	"GCVLevel"	各レベルで実行される"GCV"
	"SURE"	Steinの不偏リスク推定
	"SUREHybrid"	"SURE"閾値化と"Universal"閾値化の組合せ
	"SURELevel"	各レベルで実行される"SURE"
	"Universal"	DonohoとJohnstonの普遍的閾値
	"UniversalLevel"	各レベルで実行される"Universal"

{"FDR",α}の母数条件として，α は0から1までの数でなければならない．デフォルトで，"FDR"は{"FDR",0.05}に等しい．
使用可能な短縮 tspec 形

	"FDR"	{"Soft",{"FDR",0.05}}
	"GCV"	{"Soft","GCV"}
	"GCVLevel"	{"Soft","GCVLevel"}
	"SURE"	{"Hard","SURE"}
	"SURELevel"	{"Hard","SURELevel"}
	"SUREShrink"	{"Soft","SURE"}
	"Universal"	{"Hard","Universal"}
	"UniversalLevel"	{"Hard","UniversalLevel"}
	"VisuShrink"	{"Soft","Universal"}
	"VisuShrinkLevel"	{"Soft","UniversalLevel"}

例題

すべて開くすべて閉じる

例 (2)

ノイズのあるデータのDiscreteWaveletTransform：

閾値化ウェーブレット係数でデータを平滑化する：

もとのデータと平滑化されたデータを比較する：

カラー画像からノイズを除去する：

閾値化ウェーブレット係数：

InverseWaveletTransformを使って平滑化された画像を合成し，もとのデータと比較する：

スコープ (12)

基本的な用法 (4)

WaveletThresholdはDiscreteWaveletDataオブジェクトに使うことができる：

結果は閾値化された係数を表す新たなDiscreteWaveletDataオブジェクトである：

閾値化のメソッドを指定する：

特定の閾値化関数を使う：

閾値の選び方も指定する：

逆変換をして比較する：

ウェブレット係数への影響を可視化する：

WaveletListPlotを使って比較する：

特定のウェーブレット指標について閾値化を行う：

デフォルトで，詳細化係数のみが閾値化される：

Automaticを使って逆変換に使われた係数を閾値化する：

Allを使ってすべての係数を閾値化する：

{wind₁,wind₂,…}を使ってどの係数を閾値化するかを完全の制御する：

結果の係数を比較する：

閾値化メソッド (8)

ノイズのあるデータを自動閾値化メソッドを使って平滑化する：

すべての名前付き自動閾値化メソッド tspec を比較する：

特定の閾値化関数 tfun を選び，適用する：

自動的に選択された閾値を使って閾値化された係数からデータを再構築する：

閾値の自動計算に名前付きのメソッドを使う：

さまざまな閾値の選択メソッドで"Soft"閾値化した後，データを再構築する：

特定の数値による閾値を使う：

最高の平滑化はノイズの尺度に似ている閾値で得られる：

関数を使って閾値を計算する：

標準偏差より下のすべての係数を閾値化する：

-0.5から0.5までの範囲の係数値に対する閾値化関数 tfun の効果をプロットする：

さまなざな尺度の異なるデータに細分化の各レベルで閾値化を別々に適用する：

各レベルで別々の閾値を選ぶ別々の方法：

全レベルに1つの閾値を選ぶメソッドと比較する：

を計算するために関数とウェーブレット指標を指定することで閾値化を行う：

標準編纂より下のすべての詳細化係数を閾値化する：

一般化と拡張 (1)

FindThresholdを使って閾値を計算する：

閾値化関数を指定することで閾値非依存のレベルを計算する：

アプリケーション (8)

自動ノイズ除去 (2)

単純な自動平滑化のためのデータ処理パイプライン：

1Dデータのノイズを除去する：

2Dデータのノイズを除去する：

標準偏差 σ の正規分布に従うノイズを加える：

異なるノイズレベルでの自動平滑化の効果を比較する：

画像効果 (1)

画像の特定の成分を閾値化する：

水平および垂直詳細化係数{___,1|2} のみを強力に閾値化する：

係数を比較する：

逆変換の画像には主に対角の特徴がある：

ベンチマーク閾値化法 (2)

自動閾値を持つ異なる閾値化関数 tfun で差し引かれたノイズをプロットする：

（ノイズのモデルを与える）もとのデータから平滑化されたデータを差し引く：

ノイズのあるデータを平滑化する際の自動閾値化メソッドのパフォーマンスを比較する：

SNR（信号対ノイズ比）とピークSNRを使って（単位：dB）パフォーマンスを量化する：

閾値化メソッド th を詳細化係数{___,1}に適用して平滑化する：

すべての名前付き自動閾値化メソッドを比較する．値は高い程よい：

平滑化されたデータを完全にノイズがないデータとともにプロットする：

閾値計算 (3)

"Universal"閾値：

LiftingWaveletTransformを実行する：

平均絶対偏差は第1細分化レベル{1}で詳細化係数を使って計算される：

普遍的閾値をとして計算し，"Hard"閾値化を行う：

WaveletThresholdを使って"Universal"閾値を計算する：

閾値を比較する：

"SURE"閾値：

LiftingWaveletTransformを行う：

"SURE"閾値を計算する：

WaveletThresholdを使って"SURE"閾値を計算する：

閾値を比較する：

"FDR"閾値：

LiftingWaveletTransformを行う：

ノイズレベルを推定する：

各ウェーブレット係数について，その両面値を求める：

サイズに基づいてを順序付ける．を求める．ただし，は有意水準である：

閾値をとして計算する：

WaveletThresholdを使って"FDR"閾値を計算する：

閾値を比較する：

特性と関係 (9)

閾値が小さいと閾値化関数はIdentityに近付く：

"Hard"閾値化はChopに似ている：

閾値より小さい絶対値を含むデータ値は0に設定される：

"Soft"閾値化は縮小操作を行う：

一定の閾値より小さいデータ値は0に設定される．より大きい値はだけ縮められる：

"Firm"閾値化：

母数 ()は強い閾値化が0からIdentityの間で補間する範囲を制御する．母数 ()はがをデフォルトとしてからの間に収まる範囲を制御する：

の異なる設定値：

の異なる設定値：

の異なる設定値：

"Firm"閾値化は"Hard"閾値化と"Soft"閾値化を折衷したものになる：

"Firm"閾値化は"Hard"閾値化よりも一様に分散が小さい：

極限では，"Firm"閾値化は"Soft"閾値化を行う：

極限では，"Firm"閾値化は"Hard"閾値化を行う：

"PiecewiseGarrote"閾値化：

これは母数がの1つだけという利点を持つ"Firm"閾値化に似ている：

"SmoothGarotte"閾値化：

極限では，"SmoothGarotte"は"Hard"閾値化になる：

"Hyperbola"閾値化：

WaveletMapIndexedを使って"Hard"閾値化を行う：

考えられる問題 (3)

"GCV"閾値を持つ"Hard"閾値化関数を使う：

ノイズ係数は"Hard"閾値化を通ることがある：

"Soft"閾値化関数は偽のピークを縮める：

ノイズ推定第1レベルの詳細化係数に基づいて計算される：

推定ノイズのレベルが0のときは警告が発せられる：

WaveletThresholdは非数値的ウェーブレット係数には作用しない：

トップへ