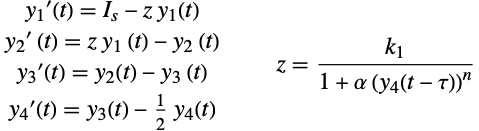遅延微分方程式

常微分方程式との比較と相違ステップのメソッド
不連続性の伝播と平坦化例題
履歴データの保存

遅延微分方程式とは，現時点の時間導関数が解だけでなく，前の時間における導関数にも依存する可能性のあるような微分方程式である．

単純な初期条件では，初期の履歴関数 を指定する必要がある．数値 および は遅延，もしくは時間差と呼ばれる．遅延は定数，関数 および の （時間依存性遅延），関数 および （状態依存性遅延）である場合がある．導関数の遅延 を伴う遅延方程式は中立型遅延微分方程式(NDDE)と言われる．

NDSolveの方程式処理コードは，遅延方程式を数学表記に入れることができるよう設計されている．

x[t-τ]遅延 τ の従属変数 x
x[t /; t≤t0]ϕt0より小さい t についての式 ϕ として初期履歴関数を指定する

遅延と初期履歴の入力

現在NDSolveにおける遅延方程式の実装は，定数遅延のみをサポートする．

二階遅延微分方程式を解く：
解とその最初の2つの導関数をプロットする：

簡単にするために，このドキュメントでは積分は常に小さい方から大きい へ進むと想定して書いてある．しかしNDSolveは，初期履歴関数が より大きい値に与えられ，遅延が負である場合は，逆の方向の積分をサポートする．

負の の方向で二階遅延微分方程式を解く：

常微分方程式との比較と相違

遅延微分方程式は常微分方程式によく似ているが，それぞれの理論はもっと複雑であり，驚くほど異なる点もある．このセクションでは相違点をいくつか挙げてみる．

異なる初期履歴関数 の解を見てみる：

初期関数が を満足する限り，のときの解は常に1である[Z06]．常微分方程式では，初期条件を得るために解から逆方向に積分できる．

パラメータ の異なる値に対する の解を調べてみる：

のとき解は単調であり， のとき解は振動し， のとき解はリミットサイクルに近付く．もちろんスカラーの常微分方程式の場合は，解は に独立な単調である．

2つの付近の定数初期関数について，Ikedaの遅延微分方程式 を解いてみる：
解のプロットである：

この簡単なスカラーの遅延微分方程式には，カオス的な解があり，上で示されている動きは非常にブラウン運動に似ている[S07]．遅延 は を超えて増加されたので，リミットサイクルが現れ，最終的に となる前にカオスを導くカスケードを倍増する区間が続く．

，，の解を比較する：

遅延方程式では安定性もかなり複雑である．線形常微分方程式の検定方程式である は，ならば漸近的に安定した解を持ち，ならば不安定であるということが広く知られている．

これに一番近い遅延微分方程式は である．たとえ実数の と だけを考えたとしても，状況はそんなに簡単ではない．これを示す解のプロットを以下に挙げる．

と のときは，解は安定である：
と では解は不安定である：

したがって，解は の値次第で では安定し，では不安定になる可能性がある．次ではManipulateを設定し， 平面を調査してみる．

および を変化させて調べてみる：

不連続性の伝播と平坦化

遅延によりどのように不連続性が伝播するかというのが遅延微分方程式の重要な特徴であり，それを解く数値的な方法に大きなな影響を与える．

のとき について を解く：

上の例では は連続であるが，において に第一種不連続がある．これは，左から近付くと，初期履歴関数 の導関数により与えられる値がであるが，右から近付くと値は遅延微分方程式により与えられ となるからである．

付近でにおける の連続性によりであるため は において連続である．

方程式を微分すると と結論付けることができるため， には において第一種不連続があるのである．上と本質的に同じ理論で，において第二導関数は連続であるといえる．

同様に，は において連続である．言い換えると， は において 倍微分可能ということである．これは平坦化と呼ばれ，一般に非中立の遅延方程式に当てはまる．平坦化は区間につき一階よりも速いこともある[Z06]．

中立遅延方程式の場合，状況は全く異なる．

のとき について を解く：

解が 連続で区間的であることは簡単に分かる．しかし，次の

では，すべての非負の整数において非連続点がある．

一般に中立遅延微分方程式の不連続性の平坦化は存在しない．

不連続性の伝播は，数値ソルバの観点からすると非常に重要である．もし不連続の可能性のある点が無視されると，ソルバの次数は減る．もし不連続点が既知であれば，不連続点までだけを積分し，その点をちょうど越えたところで新しい関数値でメソッドを再開させることで，より正確な解が得られる可能性がある．これだと解の滑らかな部分で積分法が使われるため，正確なステップが多くなり，拒否されることが少なくなる．指定された不連続点から，遅延により今後の不連続点が判明し，発見されるイベントとして扱うことにより検出されることが可能である．

複数の遅延がある場合，不連続性の伝播は非常に複雑になることがある．

2つの遅延を含む中立遅延微分方程式を解く：
解をプロットする：

このプロットから，中立遅延 から想定されるような非負の整数における不連続性があるというのは明らかである．しかし，第二および第三導関数を見ると，における第一不連続性から伝播された ，， のような点に関連した不連続性もあることが分かる．

第二導関数をプロットする：

実際，前向きに伝播された不連続性の木がある．解の区間に対する不連続の木を見付け，表示する方法は，次のセクションで説明する．

不連続性の木

指定された遅延を持つ遅延微分方程式の伝播された不連続性のグラフを与えるコマンドを定義する：
上記の例で までの不連続性の木を得る：
次数 の不連続性に対する と のプロットを示すコマンドを定義する：
層グラフとしてプロットし，各不連続点のツールチップとして不連続性プロットを表示する：

履歴データの保存

一旦解が最初の不連続点を越えると，計算されなければならない遅延された値の中には初期履歴関数の領域外のものもあり，計算された解は通常前のステップとの間を補間することで値を得るために使われる．遅延微分方程式の解が正確であるためには，補間がメソッドと同じくらい正確でなければならない．これは常微分方程式の積分方法に対する密な出力（NDSolveでオプションInterpolationOrder->Allを使って得られる出力）を使うことで達成できる．NDSolveにはほとんどのメソッドの密な出力を得るための一般的なアルゴリズムが備わっているので，どのメソッドも積分器として使うことができる．遅延微分方程式のデフォルトを含めて，メソッドの中には一般的な方法よりもほとんどの場合ずっと効率よく密な出力を得る方法が備わっているものもある．"DifferenceOrder"->3の"ExplicitRungeKutta"のような十分低い次数のメソッドでは，三次エルミート多項式を密な出力として使うことができるので，履歴を維持するのに余分なコストがかからない．

履歴データは頻繁に評価されるので，どのステップ間を補間しなければならないかを決めるための迅速な検索メカニズムを持っている必要がある．NDSolveでは二分探索法が使われ，検索時間は実際の関数評価のコストに比べると無視できるほどである．

成功したそれぞれのステップのデータは次のステップに移る前に，効率的に拡張できる形式で保存される．NDSolveが解を生成すると，このデータを使いInterpolatingFunctionオブジェクトに再構成するだけなので，遅延微分方程式の解は常に密な出力として返される．

ステップのメソッド

定遅延では，決まった時間内に不連続点すべての集合を得ることが可能である．ステップのメソッドという考えは，単にその区間上の滑らかな関数を積分して，確実に右から関数を再評価するようにして次の区間を開始するというものである．区間が小さすぎない限りこのメソッドはうまく動作する．

NDSolveに現在実装されているメソッドは，ステップのメソッドに基づいている．

ステップの記号的メソッド

このセクションではメソッドがどのように動作するかを例示するステップの記号的メソッドを定義する．ここではコードを簡単にして，的を得たものにするため，実際の引数チェックを行わないことに注意する．また履歴のデータ構造と検索も効率的ではないが，記号的な解の場合はたいした問題にはならない．

DSolveを使って，解が滑らかな区間上で積分する：
Piecewise関数を返すステップの方法関数を定義する：
である遅延微分方程式 の解を見付ける：
解をプロットする：
NDSolveで見付かった解の質を厳密解と比べることでチェックする：

このメソッドは中立遅延微分方程式でも使える．

の中立遅延微分方程式 の解を見付ける：
解をプロットする：
NDSolveで見付かった解の質を厳密解と比べることでチェックする：

DSolveが解を見付けることができる限り，記号的メソッドも記号的パラメータで使用できる．

記号的定数を持つ簡単な線形遅延微分方程式の解を見付ける：

コードがリストも取れるように設計されている理由は，系でも使えるようにするためである．

遅延微分方程式の系を解く：
解をプロットする：
NDSolveで見付かった解の質を厳密解と比較することによりチェックする：

このメソッドは不連続性の木を計算するので，複数の定遅延にも使える．しかし複数の遅延があると，解はすぐにかなり複雑なものになりDSolveは大きい式で行き詰ってしまう．

2つの遅延を持つ非線形の中立微分方程式を解く：
解をプロットする：
NDSolveで見付かった解の質を厳密解と比べることによりチェックする：

例題

遅延のあるロトカ・ボルテラ方程式

ロトカ・ボルテラ系はある動物種が他の種に及ぼす影響が連続的で即時的であると仮定して，動物種の成長とかかわりをモデル化する．一つの種の他の種に対する遅延した影響はインタラクションの項に時間差を導入することでモデル化することができる．

以下の系

を考えてみる．遅延がない場合 と系(1)はすべての に対して一定である不変量 を持ち，中立に安定した周期解がある．

この解を遅延ありとなしで比較してみる：

この例では，ほんのわずかな遅延でも周期軌道を不安定にするという影響がある．遅延のあるロトカ・ボルテラ系の異なるパラメータを使うと，大域的な引力平衡があることが示される[TZ08]．

酵素反応

以下の系

を考える．これは酵素反応をモデル化したもので は一定レベルで維持された基質供給であり，最終産物 の 分子が反応ステップ を禁止するものとする[HNW93]．

この系は ，， のとき均衡である．

均衡から離れたところで小さい摂動を開始して(1)の解を調べる：

マッキー・グラス(Mackey–Glass)方程式

マッキー・グラス方程式 は，白血球細胞の生成をモデル化するために提唱された．

次はマッキー・グラス方程式の周期解である．このプロットは過渡解がなくなるようの後にのみ表示される：
以下はマッキー・グラス方程式のカオス解である：
次は解を3D に埋め込んだものである：

カオス解の確度をチェックすると面白い．

別のメソッドでカオス解を計算し，異なるメソッドで計算された の間の差分 に対するをプロットする：

区間の最後までにはメソッド間の差分は次数1になる．カオス系では偏差が大きいのが通常であり，実際のところ大きい区間に対して非常に正確な解を得ることは不可能であるか必要ないことである．しかし，高質の絵画得たければ，NDSolveでより高い精度を使うことができる．精度の高い遅延微分方程式では，"StiffnessSwitching"メソッドが推奨される．

高精度と高許容誤差のカオス解を計算する：
最終回付近の3つの解をプロットする：