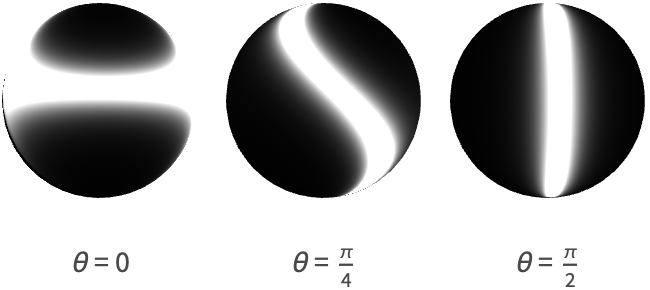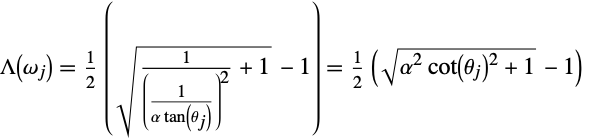物理ベースレンダリング
物理ベースレンダリング(PBR)とは現実世界の光の挙動をモデル化することによって画像を描画しようとする,コンピュータグラフィックスのアプローチである.PBRは物理ベースシェーディング,カメラ,光等の多様な領域をカバーする総称である.
物理ベースシェーディング(PBS)はPBRの主要コンポーネントであり,Wolfram言語ではMaterialShadingとして実装されている.このドキュメントでは,その実装およびその根底にある理論を扱う.
動機
物理ベースレンダリングの手法は3Dグラフィックスプログラムでは当たり前になっている.PBRは,純粋に芸術的なテクニックよりも以下の点で優れている.
1. 物理的な正確さ — PBR手法は実際の光の挙動により類似しているので,その手法を利用するパイプラインはより写真のようにリアルな描写でのレンダリングが可能である.
2. 直感的なパラメータ化 — PBRシェーダのパラメータは純粋に美的な値ではなく物理特性に基づいている.このため,パラメータを現実世界のマテリアルに合うように調整するのが簡単になっている.また,物理的に無理なマテリアルを作成するのは難しい.
3. 移植性 — 最新のグラフィックスプログラムはほとんどPBRマテリアルをサポートしており,その実装はどのプログラムでも同様である傾向がある.したがって,1つのレンダリングプログラムのパラメータを別のプログラムにコピーして同じ結果が得られることがよくある.
物理的正確さ
ほぼすべてのレンダリングの実装は,多かれ少なかれ物理ベースである.PBRが他と異なる点は,特性や法則を着実に実行するという点である.これには以下の点が含まれる.
1. エネルギー保存 — 受ける以上の光を反射する面はない.
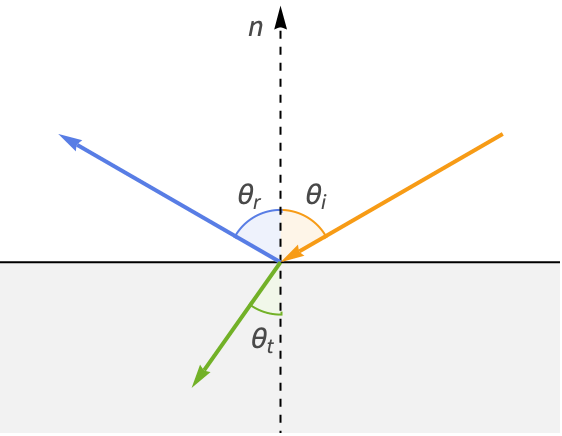
4. フレネル(Fresnel)方程式 — 光はフレネル方程式に従って物質の界面で反射し屈折する.
5. ヘルムホルツ(Helmholtz)の相反性 — 光線は向きに関係なく,同じ経路に従う場合は同様に動作する.これにより観測点から光源までの光線を正確に「追跡」することができる.
これらの特性の影響についてはこのドキュメントで詳しく述べる.
制約
PBRは,光を個々の光線としてモデル化する幾何光学(光線光学とも言われる)を使って光のシミュレーションを行う.このモデルは,異なる物質の界面における反射や屈折を除いて,光線がまっすぐ進むことを想定している.
このモデルは簡約されているため,以下のようないくつかの面は無視される:
• 偏光 — 偏光はある面に当たると異なる動作をすることがある.
• 干渉 — 別々の光波は干渉して互いに打ち消し合ったり増幅し合ったりすることがある.
• 相対性理論におけるドップラー(Doppler)効果 — 高速で移動するオブジェクトは,表面で反射された光波の波長を変化させることがある.
• 重力レンズ — 光の方向は重力によって変わることがある.
このようなことがあっても,PBRは多様なマテリアルの説得力のあるシミュレーションが行える.
レンダリング入門
PBSの中心となる問いは,オブジェクトの表面を離れる光の量と方向の両方をどのように決定するかということである.この問いの重要性を理解するために,このセクションでは,この情報がシーンの描画にどのように使えるかを説明する.
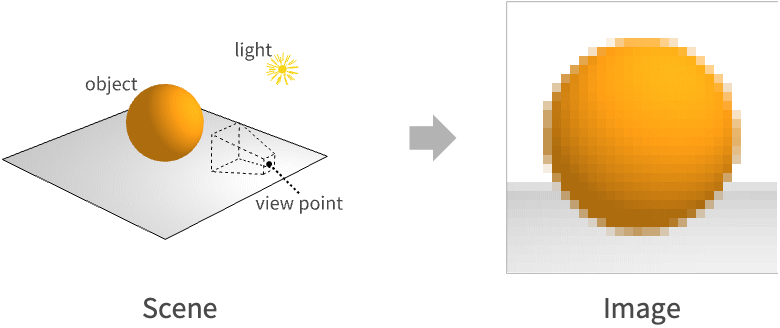
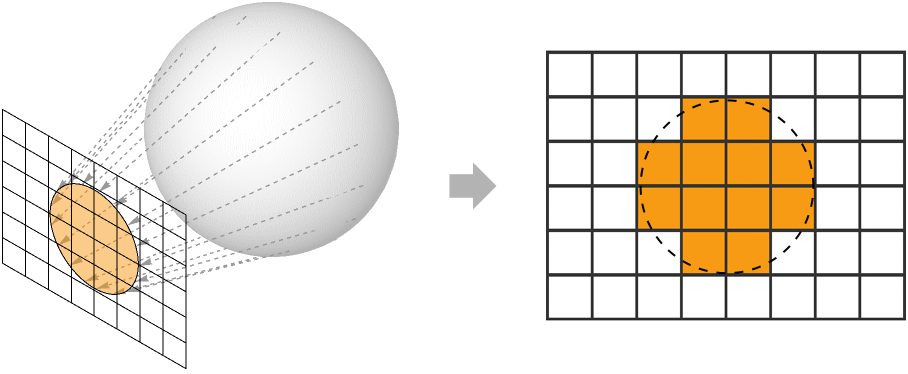
3Dコンピュータグラフィックスでは,レンダリングは3Dシーンの数学的表現を2D画像に変換するプロセスである.この画像は画素の長方形格子からできており,色は個々に計算される.画素の色を計算するプロセスは「シェーディング」と言われる.
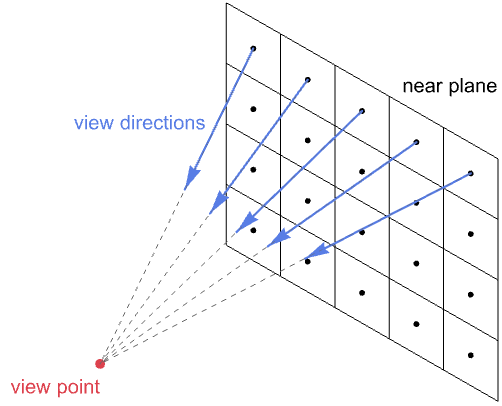
これらの画素は,視点の目の前にある小さい平面の3Dシーン内に埋め込まれていると考えることができる.この平面は「最前面」と呼ばれる.各画素は,その中心から視点に向かう,対応する視線方向ベクトルを持つ.
画素の色は,視線方向に沿って画素の中心を通り抜ける入射光の量で決まる.画素に入ってくる光は,直接表面から放射されても他の光源からのものが反射されても,シーンのオブジェクトの表面から来なければならない.光は直線で進むと仮定しているので,どの画素もその中心を通過して視線方向に沿った光を移動させるシーン内で多くて1つの表面の点を持つ.*
*これはすべての面が不透明であると想定している.透明な面の場合は複数の点を考慮する必要がある.
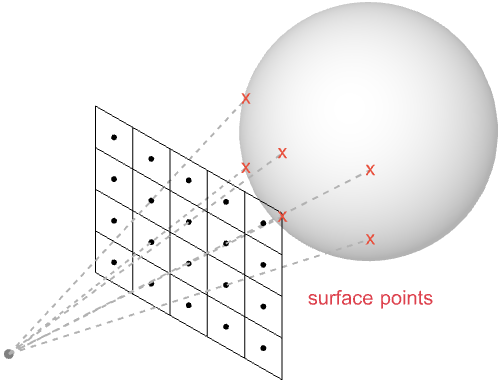
与えられた画素に対応する表面の点を決める一般的な方法が2つある.オフラインレンダリングでは,画素の中心から負の視線方向に沿った光線を投じるのに,通常レイトレーシングが使われる.光線が表面と交わる場合,対応するヒットポイントが所望の表面点である.
リアルタイムレンダリングでは,一連の線形変換をシーンの形状に適用することによって,すべての面を最前面に投影する方法がもっともよく使われる.この後でラスタライズと補間を行って各画素に対する正確な表面の点を決定する.
使用するメソッドにかかわりなく,結果となる表面の点は同じである.
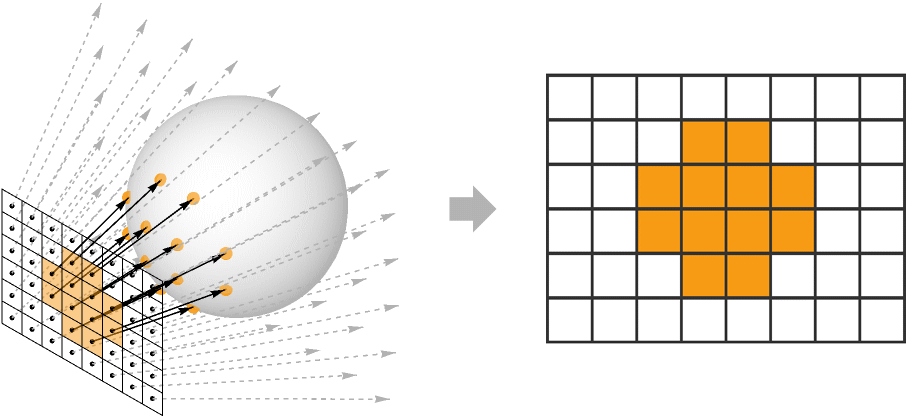
表面の点が分かると,画素の色はその点から画素の視線に沿った出射光の量によって与えられる.この出射光の量は反射方程式で決められる.
反射方程式
シーンの中の光の大域的分布はレンダリング方程式で記述される.PBRではこの方程式の局所的なものを反射方程式と呼ぶ.
高レベルにおいて,不透明な表面の反射方程式は以下で定義される.
この方程式は,表面上の点 ![]() から特定の方向
から特定の方向 ![]() への出射光の量を記述する.この光の量は,その点の「放射輝度」と言われる.
への出射光の量を記述する.この光の量は,その点の「放射輝度」と言われる.
放射輝度はスペクトル量である.つまり,これは光のさまざまな波長(色)から成り立っている.現実世界の光源の測定値を取るとき,放射輝度は分光分布を使って記述されることが多い.分光分布は,可視スペクトル全体の光の強さを与える.
これらの分布上の計算を保存したり実行したりするのは計算的に高価である.その代りにグラフィックスプログラムで放射輝度を3Dベクトルとして保存する.3Dベクトルのチャンネルは光の赤,緑,青の波長の強さを意味する.人間が色を認知する方法のため,この3つの光の波長を組み合せると,ほとんどの可視スペクトルが形成できる.
反射方程式を見ると,出射光の放射輝度は表面によって放射された光とそれによって反射された光の和である.以下のセクションでは,この2つの光について詳しく説明する.
放射光 (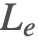 )
)
放射光は表面自体によって生成された光である.現実生活では,これは多くの場合,熱いオブジェクトが光る現象を引き起こす黒体放射の結果である.
ほとんどのグラフィックスプログラムでは,この光はRGBカラーの形式でユーザによって指定される.指定された色が返されるだけなので,放射光の量を決めることは自明である.
Wolfram言語のデフォルトの照明システムでは,放射光はGlowで指定される.MaterialShadingには"EmissionColor"パラメータが使われる.
反射光 (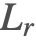 )
)
反射光には,シーンの別のところから表面の点に入射し,出射方向に向け直されるすべての光を含む.ほとんどのオブジェクトは人間の可視スペクトル内の黒体放射が起こるには冷たすぎるため,反射光によって人間は見ることができていると言える.
反射光項が,以下のような完全な積分形式に拡張されることはよくある.
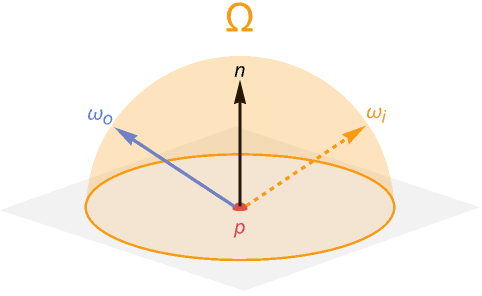
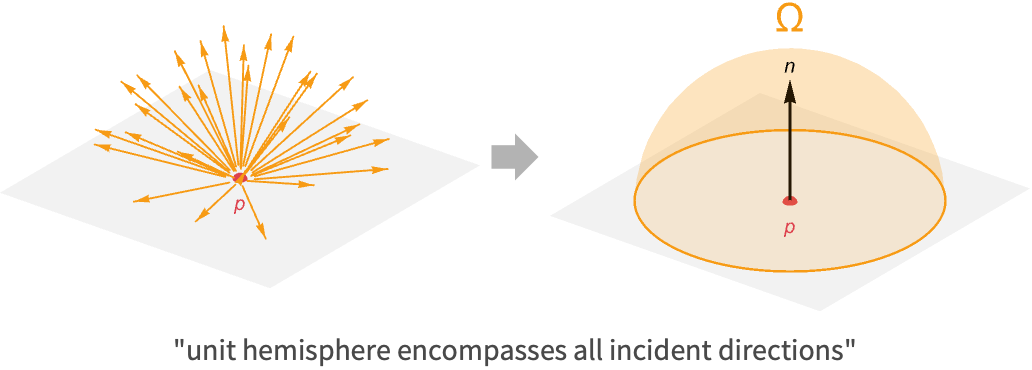
指定された表面の点の入射光が入ってくる可能性のある方向すべてを考えなければならないという点で積分になる.このような方向すべての集合は,面がこの点において垂直になるよう配置された単位半球で記述することができる.この半球外の方向はすべて面の裏から来るものなので,不透明のマテリアルの放射輝度には関与しない.
残念ながらこの積分は,任意シーンについては解析的に解くことができない.代りに,積分は数値近似するか,積分を簡約するために追加の仮定を作るかしなければならない.
レイトレーシングを使うオフラインレンダリングで広く使われる数値近似法は半球上でモンテカルロ(Monte Carlo)サンプリングを行うことである.この後で,最終的な画像をきれいにするためのノイズ除去を行う場合がある.重点サンプリング等の他の最適化を使って,必要なサンプル数を減らすことができる.
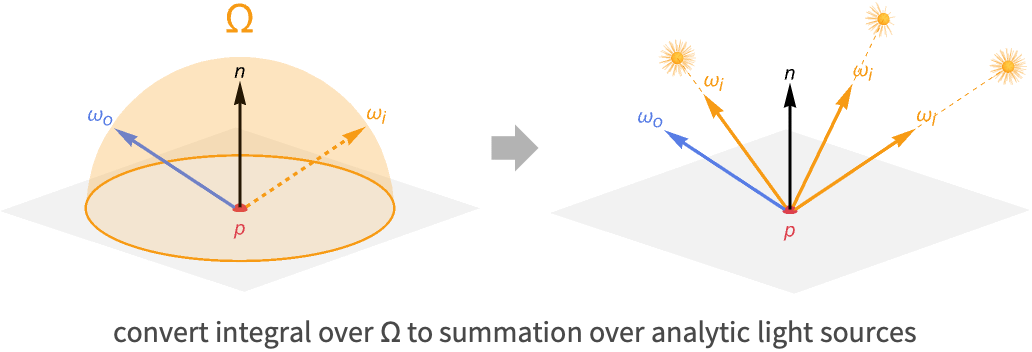
リアルタイムの適用により,積分が解析的に解かれることを可能にする,光源に関する仮定が簡約される.この仮定は表面に入射する光は,シーンの他の表面からではなく,特別な光源からのみ来ることができるというものである.この特別な光源は分析光源と言われる.その代表的なものに指向性ライト,ポイントライト,スポットライトの3つがある.
分析光源だけを使うことによって,半球上の積分はシーンのすべての光源の和に変換できる.
これで反射光について計算的に可能な式ができたので,和に含まれる3つの項を扱うことができる.以下のセクションではこれらの項について詳しく述べるが,まずは以下に短くまとめる.
![]() 項は,残り2つの項によって減衰させられた最大放射輝度として考えることができる.
項は,残り2つの項によって減衰させられた最大放射輝度として考えることができる.
入射光 (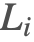 )
)
入射光項は与えられた光源から特定の表面の点までの放射輝度を与える.エネルギー保存によって,この項はこの光源から表面によって反射することのできる最大放射輝度を表す.
分析光源の放射輝度はタイプによって異なる.Wolfram言語では,それぞれの光源の放射輝度は以下のように定義されている.
2. ポイント — 放射輝度は光源への距離によって減衰した色
3. スポット — 放射輝度は光源への距離と角度の両方によって減衰した色
以下の例は各タイプの頭上の白色光で照らされた正方形を示している.ポイント光源とスポット光源における減衰は明らかである.
照明の指定および計算についての詳細はLightingをご覧いただきたい.
ランベルト(Lambert)の余弦則(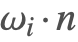 )
)
入射方向(![]() )と面の法線(
)と面の法線(![]() )の間のドット積は,ランベルトの余弦則に従って入射光の放射輝度を減衰させる.
)の間のドット積は,ランベルトの余弦則に従って入射光の放射輝度を減衰させる.
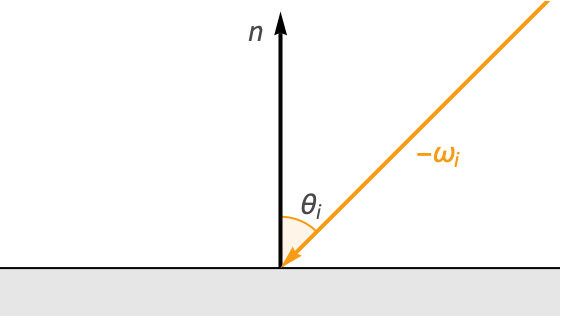
光が表面に当たるとき,表面の法線に対してなす角は入射角(![]() )と言われる.
)と言われる.
ランベルトの余弦則によると,この入射光によるこの点における拡散放射輝度は入射角の余弦(![]() )に正比例する.
)に正比例する.
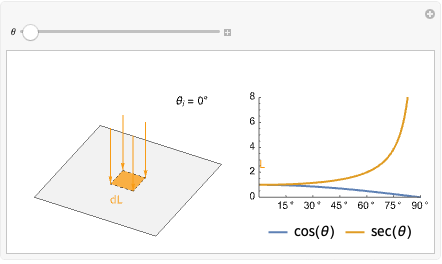
この理由を理解するために,オブジェクトの表面にある小さい2Dのパッチを想像してみよう.光線がこのパッチに表面に垂直(![]() )に当たったとすると,その光線の放射輝度はすべて小さいパッチに当たる.しかし入射角が大きくなるにつれて,光線の投射領域も拡大し,パッチの領域を超える.これにより光線の放射輝度は表面全体に広がりパッチが受ける放射輝度は全体的に少なくなるのである.
)に当たったとすると,その光線の放射輝度はすべて小さいパッチに当たる.しかし入射角が大きくなるにつれて,光線の投射領域も拡大し,パッチの領域を超える.これにより光線の放射輝度は表面全体に広がりパッチが受ける放射輝度は全体的に少なくなるのである.
想像しているパッチが単位正方形だとすると,投影面積は![]() に等しい.つまり,もとのパッチが受けた放射輝度は
に等しい.つまり,もとのパッチが受けた放射輝度は![]() ということである.
ということである.
入射角が90°になると光線は表面と平行になるため,パッチは放射輝度を受けることなく暗いままである.
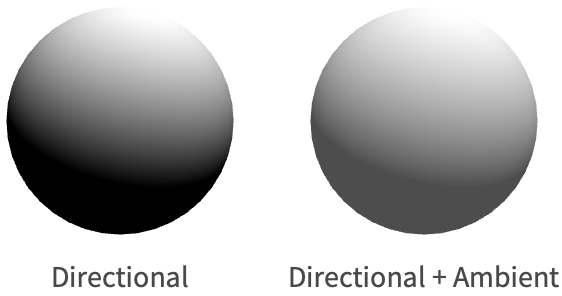
ランベルトの余弦則はつや消し面の陰影付けに関与しており,非物理ベースレンダリングの実装ではより一般的である.例えば,以下の球の照明は,上からの単独の指向性光源でランベルトの余弦則だけを使って計算される.
実際には,入射角の余弦は入射方向と表面の法線のドット積を取ることで計算される.これら2つの操作は,両方のベクトルが正規化されている限り等価である.このような理由で,反射光は余弦項を使って書かれることがあるのである.
双方向反射率分布関数( )
)
反射光の最後の項は,双方向反射率分布関数(BRDF)である.BRDFは,表面の点において出射方向に向きが変わる入射光の割合を求める.前の項と異なり,この関数はさまざまなマテリアルタイプによって異なる.
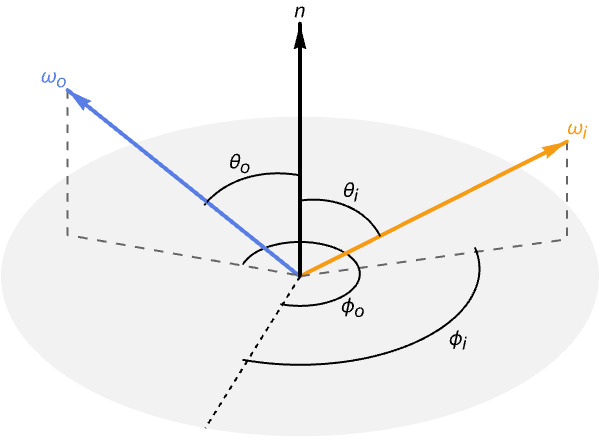
BRDFは入射方向(![]() ),出射方向(
),出射方向(![]() ),表面の法線(
),表面の法線(![]() )の3つのベクトルの関数である.表面の法線は省略されることが多いが,その場合は法線が正の
)の3つのベクトルの関数である.表面の法線は省略されることが多いが,その場合は法線が正の ![]() 軸に沿っていることが暗示される.
軸に沿っていることが暗示される.
入射光の方位角(![]() ),天頂角(
),天頂角(![]() )および表面の法線に対する出射方向を使った,同等のパラメータ化も存在する.
)および表面の法線に対する出射方向を使った,同等のパラメータ化も存在する.
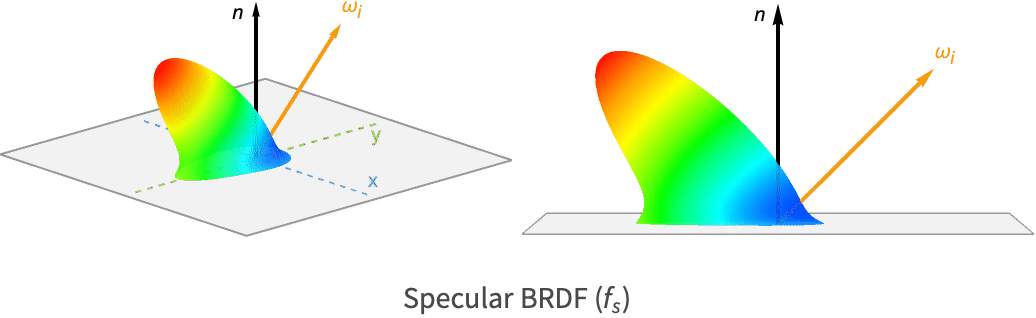
特別な装置を使うと,現実世界のマテリアルについてのBRDFを直接測定することができる.有名な例の一つにMitsubishiが行った分析がある[1].以下は1枚のPVCで測定したBRDFを示している.可視化では,入射方向は一定にして出射方向は半球全体をカバーするように変化させる.半球の大きさと色により,どれだけの光がその方向に反射されたかが分かる.
実際のマテリアルで測定されたBRDFデータを直接使うことはほとんどの場合実践的ではない.それは以下の理由からである.
1. 新しいマテリアルを測定するには,特化された装置およびそのマテリアルの入手が必要となる.
2. レンダリングに多量のデータが必要となるため,GPUのリアルタイム計算に問題が生じる.
3. 測定された各BRDFは測定されたマテリアル固有のものなので,簡単に変更することができない.
上記の理由で,グラフィックスプログラムでは,広範なマテリアルを近似することのできるパラメトリックBRDFを使うことを選択している.測定されたデータはベンチマークとして利用し,さまざまなパラメトリックBRDFモデルを比較することができる.適切なパラメータ化が見付かったら,パラメータを変更して希望のマテリアルの外観を得ることが簡単にできる.
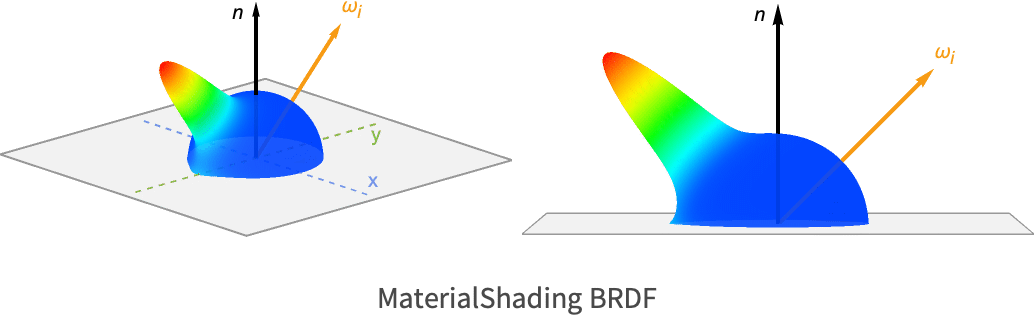
MaterialShadingによって使われる完全なBRDFの特定の例を以下に示す:
以下のセクションでは,このBRDFのさまざまな面について述べる.
2つのBRDF
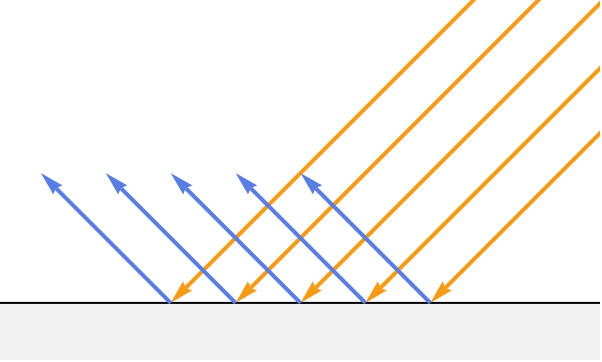
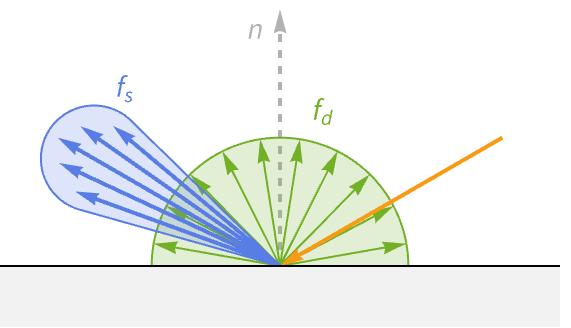
実際には,グラフィックスプログラムでは1つのBRDFではなく,合計してマテリアルの完全なBRDFを作成する2つの異なるBRDFを使っている.これらは「鏡面反射」BRDF,「拡散反射」BRDFと呼ばれ,光が表面に当たったときの2つの異なる動作,屈折と反射を表す.
反射光は,表面から理想的な反射方向に跳ね返る.一方屈折光は,光が離れていく媒質と光が入ってくる媒質両方の屈折率(IOR)によって決まる傾斜角度で表面に入る.
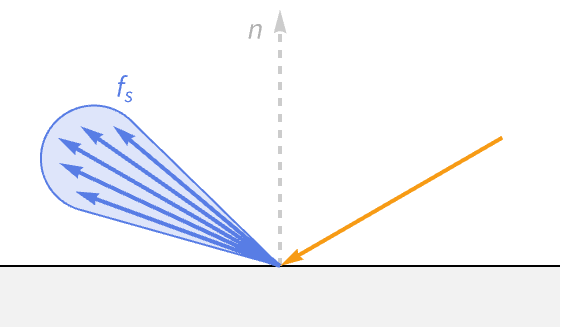
反射光
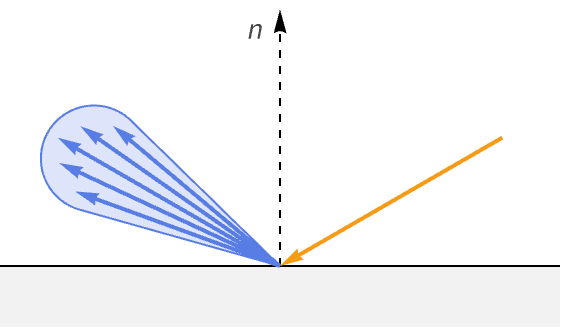
反射光は理想的な反射方向に従って表面が完全な鏡であるかのように反射する.この光は鏡面光と言われる.鏡面光は滑らかなオブジェクトに見られる明るいハイライトに関与している.ハイライトはビューアへの角度が反射の角度と並んだときに可視となる.このため,鏡面光はビューアの方向に依存する.
屈折光
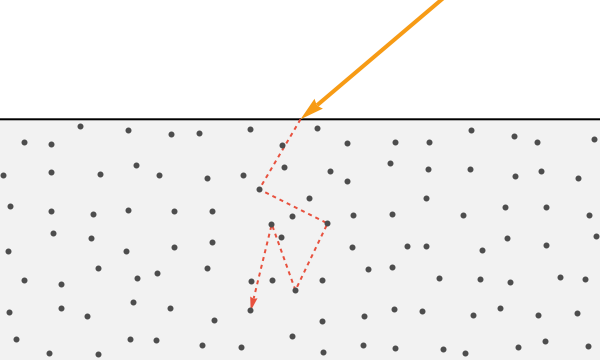
屈折光はもっと複雑な経路を辿る.表面に入った後,マテリアルの粒子と相互作用し続ける.それぞれの相互作用で光はさらに散乱しエネルギーを失う.光線がエネルギーすべてを失うと,マテリアルに吸収された(つまり,熱に変換された)ものとみなされる.
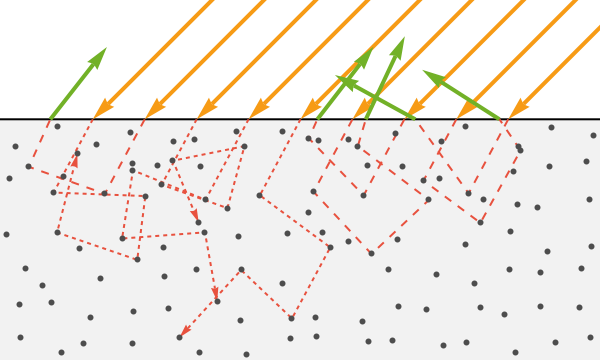
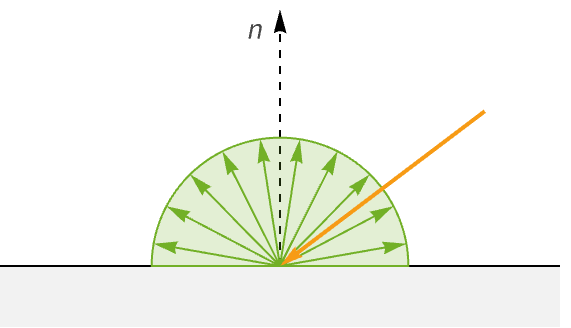
しかし散乱光のいくらかは表面から逃れる.かなりの散乱が起こった後,光の方向は実質的にランダムになる.
多量の光線が表面から逃れることを考えると,その光線はすべての方向に均等に広がっているように見える.このためこの光は拡散光と言われる.
最も不透明なマテリアルでは,屈折光は表面下数ナノメートルも突き抜けていない.つまり表面を出ていく光はその入射点の近く(1画素の幅以内)で出ていく.このため,グラフィックスプログラムでは通常,拡散光は入ってきた点から発散すると仮定している.
肌のような半透明のマテリアルでは,屈折光は格段に深く侵入し,入ってきた点からより遠い場所から出ていく.この現象は表面下散乱と言われ,追加の技法が必要となる.同様に,ガラスのような透明のマテリアルは,そのオブジェクトの裏側から出ていく前に,最小限の吸収だけで屈折光を放射する.これは透過と言い,これにも追加の技法が必要となる.
拡散反射BRDF
拡散BRDFは,光が入ってきた点に近い点で表面から逃げる屈折光の一部をモデル化する.
拡散BRDFにはランバートBRDFがよく使われるが,これはMaterialShadingによって実装されている.これは以下のように定義される:
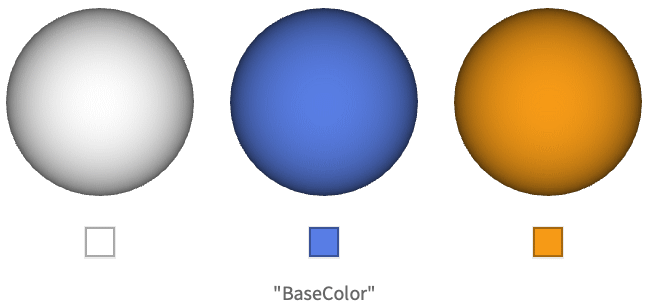
コンピュータグラフィックスでは,アルベドカラーは表面に垂直な単位放射輝度の入射光で照らされたときに表面から反射される拡散光の色を与える.つまり,照明がない表面の色である.![]() によるスケーリングはエネルギー保存のためである.
によるスケーリングはエネルギー保存のためである.
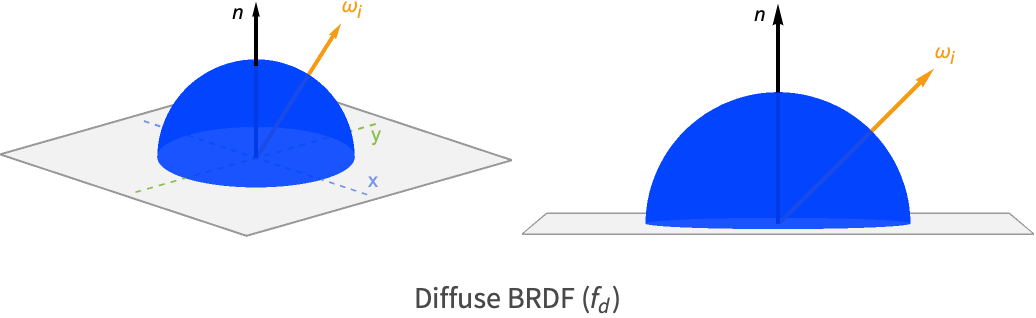
このBRDFによって形成される拡散の半球形状は,その値がビューアや光源の位置に依存しないため,普通の半球である.
MaterialShadingではアルベドカラーは"BaseColor"パラメータで指定される.
鏡面反射BRDF
拡散反射BRDFとは対照的に,鏡面反射BRDFは幾分複雑であり,最終的な方程式に至る前にある理論を知っておく必要がある.
定義によると,鏡面光は理想的な反射方向で表面から反射される光である.これが本当であるなら,球のような滑らかなオブジェクト上のハイライトは,見る方向と入射方向が並んでいる単独の無限小の点でのみ存在することになる.しかし,オブジェクトの表面の適正な部分をカバーする放光のあるハイライトを示すことがある現実のマテリアルではこのようにはならない.
この不一致はマイクロファセットの存在で説明することができる.
マイクロファセット理論
ほとんどすべての鏡面反射BRDFで使われるマイクロファセット理論は,マクロレベルでは滑らかに見える表面でもミクロレベルでは大量のマイクロファセットから成るというものである.それぞれのマイクロファセットは光学的に平坦である.つまり光線が当たると,理想的な反射方向に反射するということである.
したがって,鏡面反射の分散はこれらのマイクロファセットの方向の分散によって引き起こされる.このような理由で,マクロレベルで滑らかに見える表面は理想的な反射方向について分散した鏡面ローブが返せるのである.
物理ベースレンダリングの実装ではほぼ拡散反射BRDFが選ばれる一方,鏡面反射BRDFではさまざまなオプションが選べる.しかしどのバージョンもマイクロファセット理論を守るため,すべて以下に示すのと同じ構造に従う.
この構造には光がどのようにマイクロファセットと相互作用するかを記述する3つの項が含まれる.どのように各項が選ばれるかはグラフィックスプログラム次第であるが,通常物理的正確さと性能の間のトレードオフがある.
• 幾何項 — 他の表面部分で影になったり隠されたりしていない表面
• フレネル項 — 反射される(屈折されない)入射光の割合(パーセント)
各項を説明する前に,まずマイクロファセットの粗さと異方性の概念について述べる.
粗さ
分布項(![]() )と幾何項(
)と幾何項(![]() )のどちらも表面の粗さを記述するパラメータ
)のどちらも表面の粗さを記述するパラメータ ![]() を必要とする.マイクロファセットレベルでは,この粗さはマイクロファセットの向きの分散に対応する.マイクロファセットの向きを記述するということは,表面の法線の向きを記述することである.
を必要とする.マイクロファセットレベルでは,この粗さはマイクロファセットの向きの分散に対応する.マイクロファセットの向きを記述するということは,表面の法線の向きを記述することである.
マイクロファセットの法線が変化すればするほど光はより散乱する.![]() のとき,マイクロファセットの法線はマクロサーフェスの法線と並んでおり,このことで完全な鏡面反射が生まれる.
のとき,マイクロファセットの法線はマクロサーフェスの法線と並んでおり,このことで完全な鏡面反射が生まれる.![]() が1に近づくにつれ,マイクロファセットの法線はほぼランダムに向くため,反射光はより拡散する.
が1に近づくにつれ,マイクロファセットの法線はほぼランダムに向くため,反射光はより拡散する.
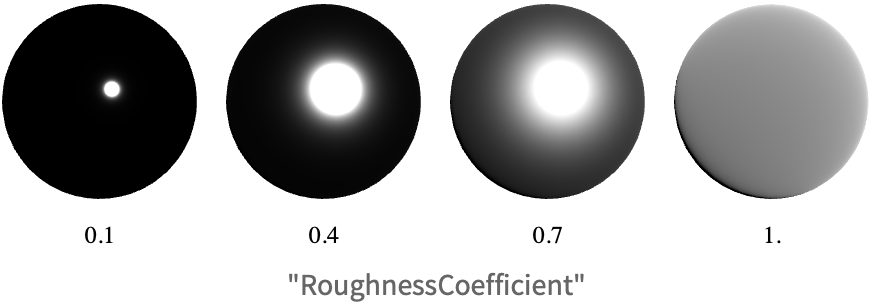
この ![]() 項を直接指定する代りに,入力として「粗さ」パラメータを取り,それを
項を直接指定する代りに,入力として「粗さ」パラメータを取り,それを ![]() に再マップして粗さを知覚的に線形にする.
に再マップして粗さを知覚的に線形にする.
この粗さパラメータはMaterialShadingの"RoughnessCoefficient"パラメータに対応する.
異方性
グラフィックスプログラムがすべてのマテリアルを等方性であると仮定することがよくある,つまりマテリアルが見られる角度にかかわらず同じように非買いrを反射するということである.マイクロサーフェスレベルでは,これはマイクロファセットの法線の向きがどの特定の方向についての優位性も見せないということを意味する.
しかし現実世界のマテリアルの中には,一方向に光を反射する強い優位性を示すものもある.これらのマテリアルは異方性と言われ,ブラシをかけた金属や木材等の素材が含まれる.
この効果は,一つは接線方向,もう一つは二重接線方向の2つの ![]() の値を考えることによって鏡面反射BRDFに実装される.これらの値はそれぞれ
の値を考えることによって鏡面反射BRDFに実装される.これらの値はそれぞれ ![]() ,
,![]() で表される.
で表される.
![]() 値のように,ユーザは直接
値のように,ユーザは直接 ![]() および
および ![]() を指定するのではなく,粗さとともに異方性の
を指定するのではなく,粗さとともに異方性の ![]() 値を計算する「異方性」という特性を渡す.
値を計算する「異方性」という特性を渡す.
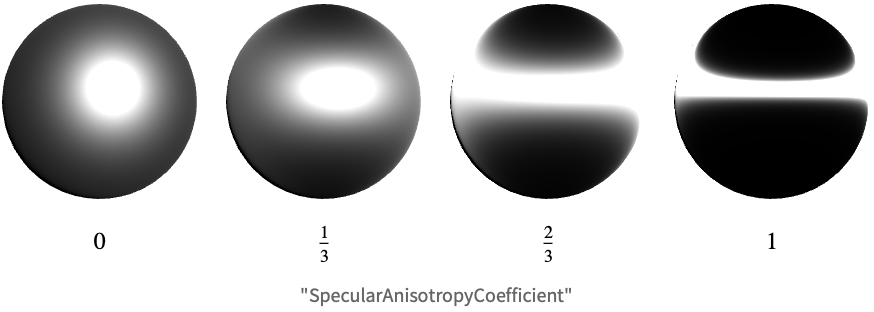
MaterialShadingでは,鏡面反射の異方性は"SpecularAnisotropyCoefficient"パラメータで制御される.
デフォルトでは,接線方向はビューアに対して水平になるように計算される.この方向は"SpecularAnisotropyCoefficient"特性で角度を指定することで調整することができる.
粗さと異方性の知識を得たところで,鏡面反射BRDFの最初の項の説明に入る.
(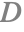 ) 分布項
) 分布項
先のセクションで見たように,鏡面光は常に理想的な反射方向(![]() )に反射する.したがって,特定の方向に表面から反射される光の量を求めるためには,まずその方向に光を反射するように向けられたマイクロファセットの比率を求めなければならない.
)に反射する.したがって,特定の方向に表面から反射される光の量を求めるためには,まずその方向に光を反射するように向けられたマイクロファセットの比率を求めなければならない.
これは,マイクロファセットの法線がマクロサーフェスの法線に対してどのように分布しているかを記述する分布項によって与えられる.この項は法線分布関数(NDF)とも呼ばれる.
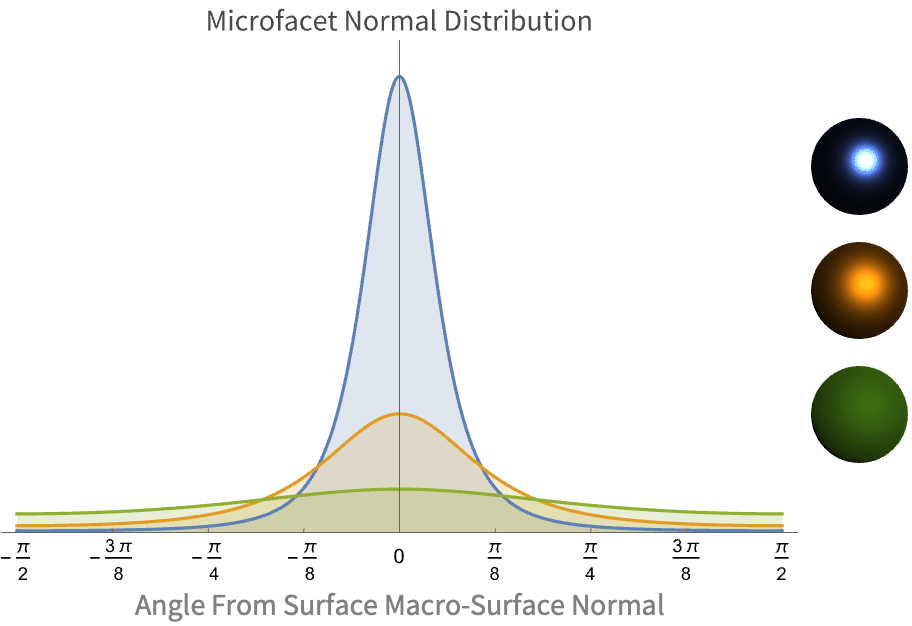
粗さのレベルを変化させたこの分布の例を対応するレンダリングとともに以下に示す.
マイクロサーフェスの法線が,マクロサーフェスの法線(プロットの0)付近にいかに集中しているかが分かる.滑らかなマテリアルの場合(青),角度が大きくなるにつれ急速に集中度が下がる.一方,より粗い表面のマテリアル(緑)では,マイクロファセットの法線がより一様に集中しており,拡散性質を物語っている.
鏡面反射BRDFはその分布から特定の角度を抽出して分布項になる.これは入射方向から出射方向に向かって光を反射する,マクロサーフェスの法線とマイクロファセットの法線方向の間の角度である.反射の法則によると,この法線方向は入射方向と出射方向の中間にある.このため,法線方向は中間ベクトルと呼ばれることが多く,以下のように計算される:
異方性マテリアルの場合,粗さは方向によって変わるため,分布項はこの中間ベクトルがどのように接線方向,二重接線方向と並ぶかを考慮する必要がある.
MaterialShadingで使われる分布項はBurley [2]である.これはウォルト・ディズニー・アニメーション・スタジオで使われているのと同じ定式であり,以下で定義される:
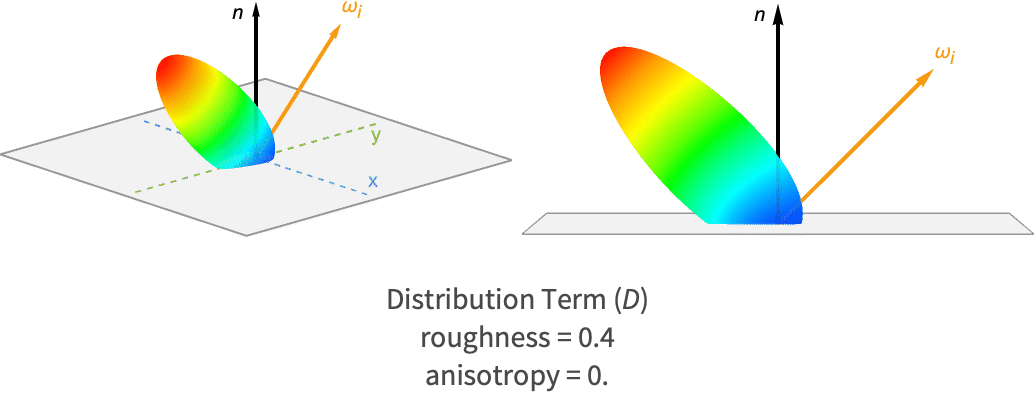
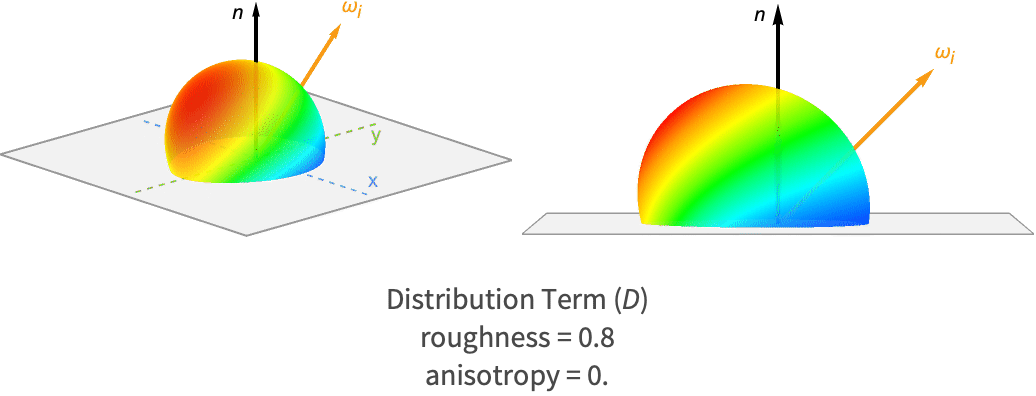
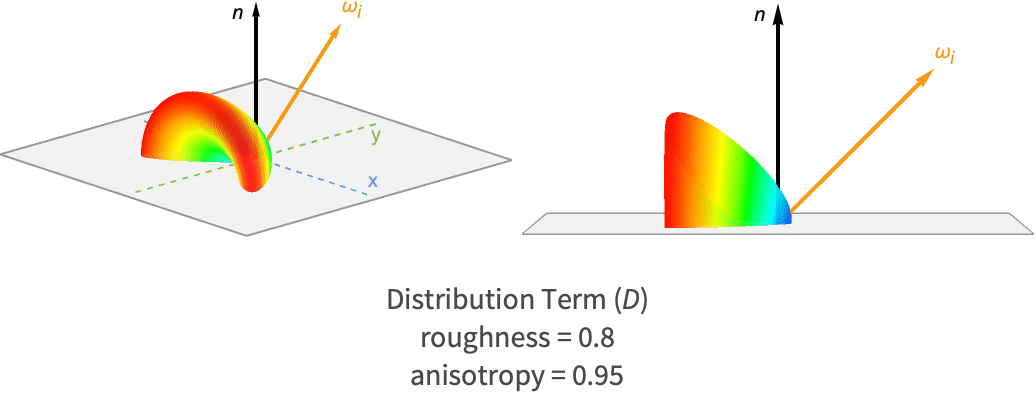
粗さと異方性を数種類組み合せた,この項だけで作られたローブを下に挙げる.
( ) 幾何項
) 幾何項
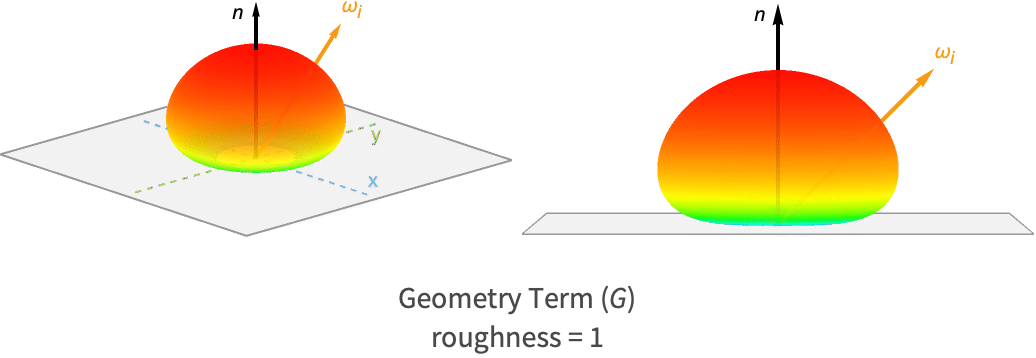
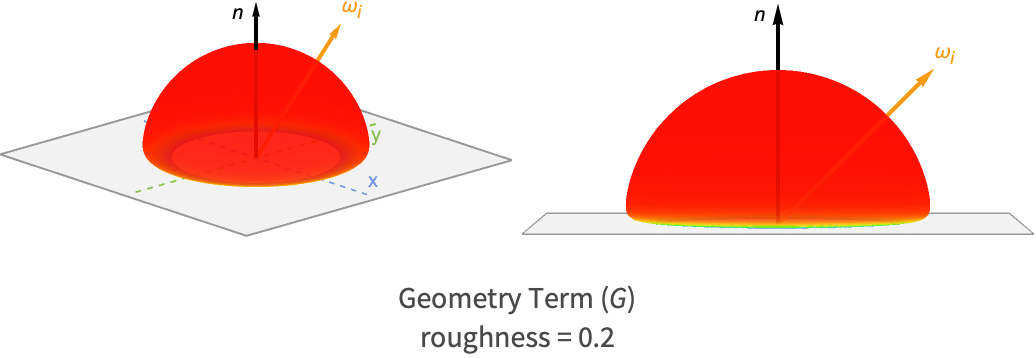
幾何項は他のマイクロファセットによって陰になったり隠れたりするマイクロファセットを考慮に入れるため,最終的な反射光には関係しない.
別のマイクロファセットが光源への経路をブロックすると,マイクロファセットは隠蔽される.同様に,マイクロファセットがビューアに見えないとき,別のマイクロファセットがそれを塞いでしまうので,マスキングが起こる
この幾何項については,MaterialShadingはGGX–Smith height-correlated masking and shadowing functionを使う[3]:
注:この項は異方性の影響を受けない.マテリアルが異方性の場合,2つの ![]() 値を平均してこの方程式のための1つの
値を平均してこの方程式のための1つの ![]() 値を得る.
値を得る.
粗い表面と滑らかな表面についての鏡面反射BRDFのこのコンポーネントに対するローブを以下に示す.
粗い表面の方が滑らかな表面と比べて,グレージング角における値がずっと小さいことが分かる.分散のないマイクロファセットはマスキングもシャドーイングも起こさないが,分散の大きいマイクロファセットは低い角度で他のマイクロファセットに対してマスキングやシャドーイングを起こしやすいためである.
(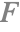 ) フレネル項
) フレネル項
先に,光がある媒体から別の媒体を通過するとき,どのように光が屈折と反射という2つの成分に分かれるかということを述べた.しかし光はこの2つの成分に常に均等に分かれるわけではない.
フレネル方程式は入射光が反射される量に対する屈折する量を記述する.この比率は入射角度と2つの媒体の屈折率の両方によって決まる.描画の目的では,これらの媒体は空気とシーンにあるオブジェクトのマテリアルであることが多い.
フレネル方程式は,光が光学的平面に入射すると想定する.したがって,光はそれぞれのマイクロファセットに個々に適用される(マイクロファセットの統計分布を想定する分布項および幾何項と異なる).
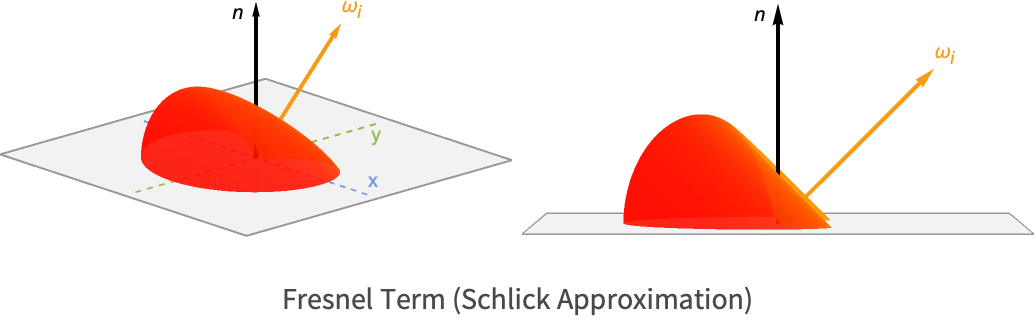
実際には,これらの方程式の近似バージョンであるシュリック(Schlick)近似を使うことが多い.
ここで ![]() は法線入射(表面に垂直に当たる光)における鏡面反射率を表し,
は法線入射(表面に垂直に当たる光)における鏡面反射率を表し,![]() はグレージング角における鏡面反射率を表す.
はグレージング角における鏡面反射率を表す.
現実では,すべてのマテリアルのグレージング角における鏡面反射率は1.0である.これはフレネル効果と言われ,大きい静水面等,大きい平面を見ると特に目立つ.
特に暗い色のマテリアルについてのシュリック近似のローブを以下に示す.反射率がグレージング角でどのように増加しているかに注目のこと.
法線入射における鏡面反射率の値を,両方の媒体の屈折率を使って正式に計算する.
ひとつ複雑なことは,マテリアルの屈折率が光の波長(色)によって変わるということである.したがって各RGBカラーチャンネルの ![]() は別々に計算する必要がある.
は別々に計算する必要がある.
実際には,![]() の3つの値はRGBカラーとしてユーザが直接指定することが多い.
の3つの値はRGBカラーとしてユーザが直接指定することが多い.
MaterialShadingは誘電性(非金属)のマテリアルにはシュリック近似を使う.値 ![]() は"SpecularColor"特性で制御される.現実世界の誘電性マテリアルでは,この値は3つの(3)カラーチャンネルすべてにおいて0.04付近と非常に低い.
は"SpecularColor"特性で制御される.現実世界の誘電性マテリアルでは,この値は3つの(3)カラーチャンネルすべてにおいて0.04付近と非常に低い.
金属マテリアルに使われる近似はもっと複雑である.その解説に入る前に,コンピュータグラフィックスにおける金属と非金属の違いについて簡単に触れておく.
導体と誘電体
物理ベースシェーディングモデルは多くの場合,金属マテリアル(導体)と非金属マテリアル(誘電体)を区別する金属ワークフローに従う.この2つの金属タイプでは拡散光および鏡面反射光の挙動が非常に異なるので,異なる計算が必要である.
誘電体(非金属)
誘電体は,プラスチック,石,木,皮等を含む,最も一般的なタイプのマテリアルである.これらのマテリアルは色を変えることなく光を反射する.しかし光が屈折すると,ある波長は吸収される一方で他は放射されるため,その色が変わる.拡散光のこの変化により,これらのマテリアルはお馴染みの色になる.例えば,バナナは光の他の波長を吸収して,残った黄色い光だけが拡散色として放たれるため黄色に見えるのである.
導体(金属)
導体には金,銅,鉄,青銅等のすべての金属が含まれる.これらのマテリアルには屈折光すべてを吸収するというおもしろい特性がある.したがって,導体には拡散色がない.導体は色を変化させるが光を反射する.金属がどのようにこの反射光を変えるかによって,人が認識するその金属の色が決まる.例えば,金は白光に黄色味を加え,銅は赤味を加える.金属が同じようにすべての波長を反射するならば,鉄やアルミニウムのように灰色っぽく見える.
(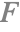 ) 導体のフレネル項
) 導体のフレネル項
鏡面ハイライトが最終的な外観にあまり影響しない誘電体には,シュリック近似が便利である.しかし導体(金属)の場合は鏡面成分がその外観すべてを形成する.したがって,導体にはより正確な近似を使った方がよい.
MaterialShadingはSébastien Lagarde [4]によって説明された誘電体-導体のフレネルの式を使う.彼の式は金属の反射性曲線を近似するために,屈折率と減衰係数の両方に依存している.
しかし,目視基準からマテリアルを一致させようとするときに,各RGBチャンネルについてこれらの特性の値を直接設定することは直感的ではない.このため,MaterialShadingは反射色とエッジの色から屈折率と減衰係数を計算する中間層も使う.反射色は表面の大部分の鏡面反射の色を記述し,エッジの色はグレージング角(通常オブジェクトの端)における光の色を決定する.
MaterialShadingはGulbrandsen [5]によって説明された反射性とエッジの色のマッピングを使う.
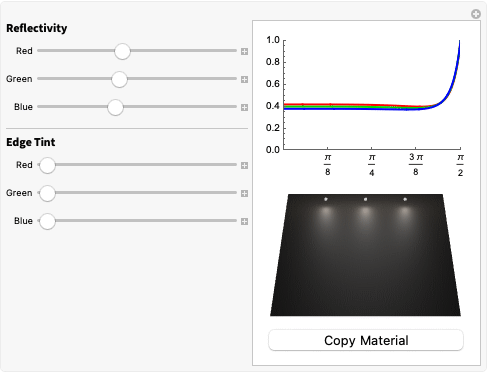
以下の例は,反射率とエッジの色のパラメータで制御された,光の赤,緑,青の波長についての反射を示している.特定の波長のエッジの色を大きくすると,その色がグレージング角において目立つようになる.
MaterialShadingでは,金属マテリアルについての反射率とエッジの色は,それぞれ"BaseColor"パラメータと"SpecularColor"パラメータで設定される.
その他の効果
ここまで見てきたパラメトリックBRDFは,不透明な単独の層のマテリアルをうまく近似する.しかし少し修正を加えると,近似できるマテリアルの種類を増やすことができる.
コート
マテリアルの中にはベースサーフェスを薄いクリアコートで覆っているものもよくある.このコートは,車や木の場合はラッカーやポリウレタンでできていることが多い.このコートを使うと反射が加わることで表面がより輝いて見える.
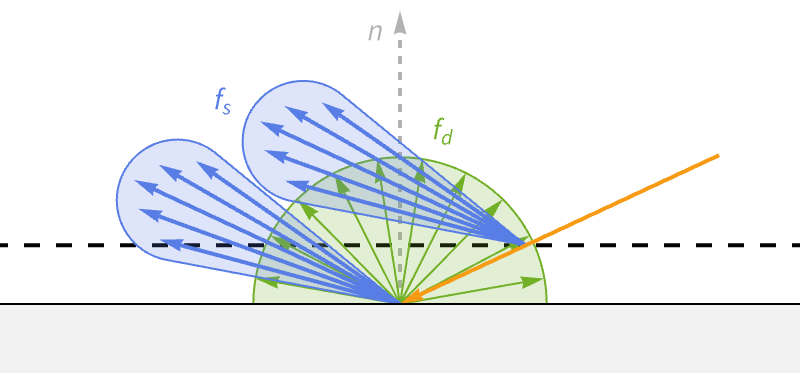
物理ベースシェーディングでは,ベースサーフェスのすぐ上に2次的な鏡面反射層があるものと仮定することによって,この効果が得られる.ここで入射光をコート層で1回,ベースサーフェスでもう1回の計2回分割する.
コーティングは非金属であると想定されるので,コート層の鏡面反射成分は誘電体鏡面反射BRDFを使う.ベース層とは異なり,コート層を通過する光は拡散ローブには関係せず,ベースサーフェスまで届き,ベースサーフェスの鏡面反射BRDFと拡散BRDFで使われる.
MaterialShadingでは,コートは"CoatColor"パラメータを使って指定することができる.コートが指定されると,追加の特性"CoatRoughnessCoefficient","CoatAnisotropyCoefficient"を使うことができる.これらはベースサーフェスの特性"RoughnessCoefficient","SpecularAnisotropyCoefficient"に対応するものである.
放光
布の中にはマクロサーフェスに垂直に立ち並んだ多数の繊維でできているものがある.グレージング角では,これらの繊維のエッジは出射方向に並び後方散乱を引き起こす傾向がある.これにより,ベルベットのようにマテリアルの縁周りにハイライトが生成される.
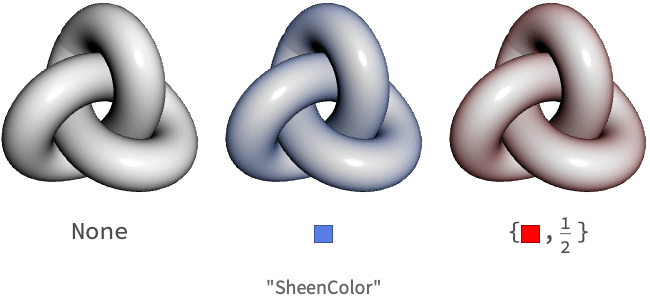
この効果は,これらのタイプのマテリアル向けの分布項を含む追加のBRDFを使うことで得ることができる.MaterialShadingはSony Pictures [6]によって記述された放光BRDFを使う.
MaterialShadingでは,放光は"SheenColor"特性を使って指定することができる.放光のある色が指定されると,放光のある光の粗さを決定するために追加の特性"SheenRoughnessCoefficient"を使うことができる.
環境光
ここまで指向性ライト,ポイントライト,スポットライトの3つの分析光源だけについて述べてきた.これらは,光源から表面に直接光を当てるため,直接光と呼ばれることもある.
しかし,現実世界では表面に入射する光のかなりの量は間接光である.これは,現在の表面に達する前に1つ以上の他の表面で反射された光のことである.この間接光のシミュレーションの過程はグローバルイルミネーション(GI)と言われ,それを実行するメソッドは多数ある.
リアルタイムレンダリングでは,安くて効率的な方法として環境項を使うというものがある.この項は反射率方程式の結果となる出射放射輝度に足して,すべての方向からの一定の入射放射輝度を近似する.Wolfram言語では,この項は"Ambient"光を指定することで設定される.
デフォルトのシステム外観とMaterialShadingはどちらも環境光をサポートする.しかし,MaterialShadingでは表面の環境遮蔽を設定することができる.
環境遮蔽は,オブジェクトの角や隙間が他の表面部分ほど間接光を受けないため,影が付いたようになる現象である.MaterialShadingでは,マテリアルの表面で受ける環境光の割合は"AmbientExposureFraction"パラメータで設定することができる.しかしこのパラメータは通常,マテリアルの隙間をオブジェクトの表面に正確にマップするために,テクスチャと一緒にのみ使われる.
参考文献
1. Ngan, A., F. Durando and W. Matusik. Experimental Analysis of BRDF Models. The Eurographics Association (2005).
2. Burley, B. Physically-Based Shading at Disney. Walt Disney Animation Studios (2012).
3. Heitz, E. "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs." Journal of Computer Graphics Techniques, Williams College (2014).
4. Lagarde, S. Memo on Fresnel Equations. 2013. https://seblagarde.wordpress.com/2013/04/29/memo-on-fresnel-equations.
5. Gulbrandsen, O. "Artist Friendly Metallic Fresnel." Journal of Computer Graphics Techniques (JCGT) 3, no. 4 (2014): 64–72.
6. Estevez, A. and C. Kulla. Production Friendly Microfacet Sheen BRDF. Sony Pictures Imageworks (2017).
7. Smythe, D. and J. Stone. MaterialX: An Open Standard for Network-Based CG Object Looks, Version 1.38, 2021.