Wolframシステム用のドキュメントのほとんどでは，主にWolframシステムで何ができるかに関して説明を行っている．どう達成するかについてではない．しかし，このページでは少し趣を変え，どのようにWolframシステムが計算処理を行うかについて多少説明を加える．より詳しい説明は「内部実装について」を参考にしてほしい．

Wolframシステムの内部処理機構を知ることは，知的な興味をそそるものではあるだろうが，それが分かって実際どのくらい役に立つかというと，最初に考えていたほどのことではないだろう．

Wolframシステムの強みのひとつは，どのように数学的な操作や他の操作がコンピュータ内部で具体的に処理されているか等の疑問を持つ必要なしに，ユーザが行いたい操作に取り組める環境を提供していることにある．

例えば，多項式 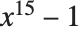を因数分解するには，ユーザは，Factor[x^15-1]と入力するだけでよい．Wolframシステムの内部コードにおいて，どんな複雑な方法で実際に因数分解が行われているか等は，ユーザは全く知る必要がない．

Wolframシステムの内部機構が実際の使用にはほとんど関係ないと，ほとんどのWolframシステムの用途に対して言うことができる．極端ではあるが，Wolframシステムを単に，特定の数学的操作等を行うための，抽象化されたシステムととらえても何の支障もきたさない．

内部でどう処理しているか分からなければ，求まる答が信頼できるものかどうか判断できないではないか，と読者によっては危惧されるかもしれない．実際に一部の操作ではそのような状況もなくはないが，ほとんどの場合は，Wolframシステムの行う計算は，数式やその他の操作を定義した規則で完全に決定されるため，そのような心配をする必要はない．

例えば，3^40は，Wolframシステムがどう内部で計算しようが，常に12157665459056928801である．

それでも，場合によっては，形式的な数学の定義に矛盾しない解が複数個存在する．例えば，記号的な積分の計算において，同じ導関数を与える複数の異なる式を得ることがある．その場合，どちらの式が実際にIntegrateにより生成されるかは，Integrateがどのように内部処理を行うかに依存する．

数値計算でも同じような現象が起ることがある．例えば，FindRootを使い方程式の根を求めることができるが，方程式によっては複数の根が存在する．その中のどれが実際に求まるかは，FindRootの内部処理の詳細による．

内部アルゴリズムへの依存度は，数値解析法をその有効範囲ぎりぎりのところで使うならばさらに増大する．

例えば，病的な積分式を関数NIntegrateに与えると，関数で使われる内部アルゴリズムの詳細に依存して，返される答は意味のあるものであったり，そうでなかったりする．

従来の数値解析システムでは，どんな計算でも，得られる結果は少なくとも名目上は同じ精度で求まらなければならないとする傾向がある．このような考え方によると，結果が正確なものかどうかは得られた結果を見るだけでは判明しない．本当に正確かどうかは，計算に使ったアルゴリズムの動作詳細を分析しないと見極めることができない，という結論が導かれてしまう．そして，この事実は人々に，数値計算に使われた内部アルゴリズムをはっきりさせることが常に重要である，というような印象を植え付けてしまっている．

しかし，Wolframシステムで取られるアプローチは違うので，上述の議論はほとんどの場合当てはまらない．つまり，多くの数値解析の問題では，Wolframシステムは任意精度による数値計算機能を使うことができるので，得られる結果はその作られるすべての桁において達成される演算の厳密な数学定義を満足する．つまり，内部処理には依存しない．

これは一般論だが，得られる答が内部アルゴリズムの詳細に依存するものであれば，その答は疑いの目で見られるべきである．他の要因が同じであっても，Wolframシステムのバージョンが違えば，違った結果を生成することがある．そのような現象が起る理由は，同じアルゴリズムでも，違ったコンピュータシステムで使うと若干異なった動作をしたり，違ったときにリリースされたバージョンでは，使われるアルゴリズムが根本的に違う場合もあるためである．

特に，複雑な問題を解く場合は，内部アルゴリズムを分析することは十分に価値あることと思えるだろう．そうすれば，どう計算を進めたら最も効率よく計算できるかが予測できる，とも考えられる．事実，まれにではあるが，そのようなアルゴリズムの分析の結果，大きな向上が得られることがある．

しかし，このような分析は，ほとんどの解法において徒労に終ってしまう．その理由として，Wolframシステムの内部機構が複雑なことがある．また，仮に特定の目的のために使われるアルゴリズムの基本動作の説明を受けたとしても，このアルゴリズムが特定の状況で実際にどう挙動するかを予測するのは通常，非常に困難である．

さらに，Wolframシステムの演算機構において各種の最適化が図られており，実際にどの最適化手段が適用されるかは計算問題の詳細により違ってくるため，計算効率も大きく変わってしまう．

式をタイプしWolfram言語に入力すると，コンピュータのメモリに，入力された式を表すためのデータ構造体が作成される．

入力したひとつひとつの式の成分は，通常，カーネルで固有のデータ構造体として扱われ，個別のメモリ領域に保管される．例えば，{2,x,y+z}とリストを入力したとする．すると，まず，リスト全体の構造を表した「骨格的情報」が特定の場所に保管され，次に，個々の成分が別の場所に保管される．

このリストの骨格的情報はちょうど3つのポインタからなり，このポインタはリストの要素を構成する実際の式の番地を指し示す．そしてそれらの式が部分式を持つならば，その部分式に対するポインタを含む．こうして，数珠つなぎになったポインタの最後に示す番地には，これ以上分解することができない最小成分の値そのものが二進数形式で保存される．

Wolfram言語の演算に対する究極的なものは x 等のシンボルの概念である．すなわち，x が参照されるたびに，新たなポインタが内部に設けられ，そのポインタ自体が x として扱われる．しかし，このポインタは同一メモリ番地を指している．この番地は，現行のWolfram言語セッションで定義されてあるすべてのシンボルを保管しておく中央テーブルと呼ばれるメモリ領域の一廓に当たる．

中央テーブルは，個々のシンボルに関するすべての情報をしまっておくところである．そこには，シンボル名の所在を示すポインタ，さらに，シンボルの評価に必要な変換規則を定義した式の所在を示すポインタが保管される．

メモリ管理は随時行われ，定義式や変数を保管する各メモリ領域について現在何個のポインタが向いているかが調べられる．アクセスするポインタ数がゼロになったとき，そのメモリ領域は必要がなくなったものとみなされ，保管してあるデータは除去され，メモリはリサイクルに回される．

こうすることで，常に実際に使われているデータしかメモリには保管されないことになり，無駄のないメモリ管理が遂行できる．

Wolfram言語の中核は，評価体と呼ばれる，単純な構造の手続きからなる．評価体は，式に現れる個々の関数を抽出し評価するためにある．

評価する関数が，およそ千個ある組込み関数のどれかであれば，評価体から直接Wolfram言語の内部コードが実行される．評価する関数に対応した操作を行い，その結果を表すための新たな式を構築するところがこの内部コードである．

Wolfram言語の提供する組込み関数は，ユニバーサルな計算にも対応できるように作られている．つまり，組込み関数を使うだけで，使用中のコンピュータ上で可能な操作なら何でもできるプログラムを組み立てることができるようになっている．

実際に試してみると分かるが，意外に少ない基本的な関数だけでユニバーサルな計算用途に対応することができる．しかし，実際にさまざまな組込み関数があるので，プログラムの構築はやりやすい．

要するに，Wolfram言語はユニバーサルな計算に対応しているので，ユーザ自身が組込み関数をカスタマイズしたりする必要は全くない．組込み関数で直接計算できない場合でも，それらを組み合せて使えば必ず計算できる．

ユニバーサルな計算という考え自体は，すべての標準的なプログラミング言語にも当てはまる．しかし，これらの多くのプログラミング言語は，コードのコンパイル作業に頼っている．ユーザがC言語またはFortranを用いるならばプログラムを記述した後に，それをコンパイルして，コンピュータ上で実際に実行できる機械語コードを生成しておく必要がある．

Wolfram言語を使えば，プログラムをいちいちコンパイルする必要はない．式を書いたなら，それを入力した時点で，式にある関数は直ちに実行される．

計算処理がより効率的に行われるように，入力された式に対して前処理（プリプロセス）が行われる．この処理のために得られる結果が変わることは全くなく，ほとんどの場合は，前処理があっても，ユーザの目に触れることはない．

Wolfram言語の持つ組込み関数には，コンピュータサイエンスおよび数学の分野で開発された非常に多くのアルゴリズムが使われている．アルゴリズムのいくつかは古くから使われてきたものだが，ほとんどのものはWolfram言語用に特別に開発したものか，既存のものを改良したものである．中でもより数学的なアルゴリズムについては，開発過程のどこかで人間の手計算で同じ問題が解かれ，アルゴリズムの計算が正確かどうか確かめられている．いずれにしても，手計算で使う手法が実際のアルゴリズムとは異なることに注意してほしい．

記号積分を例に見てみよう．手計算では，よく，変数変換や他の技法を使って積分していく．

これに対して，Wolfram言語では，記号積分は体系化されたごく少数の手法だけで計算が実行される．例えば，不定積分を求める場合は，まず，最も一般的な積分の原形が検索される．次に，見付かった原形が微分され，その微分式においてもとの積分式に釣り合った数の不確定係数が得られたかどうか判定が行われる．

上記の手順で作業が進行すると，計算の途中で，非常に複雑な代数式が生成されてしまう．時には，非常に難解な数学関数が含まれてしまう．それでも，この手順は完全に体系化されているので，手計算で使うような巧妙な技法は必要としない，という大きな利点を持っている．

だから，Wolfram言語の積分で得られる結果は，常に体系的に求められたものであると考えてよい．しかし，結果が導出される方法は，手計算の手法とは似ても似つかないものと考えてよいだろう．

同様なことが，Wolfram言語の使うほとんどのアルゴリズムに関してもいえる．一見簡単そうな演算でも，Wolfram言語内で処理されると，高等数学や計算工学の定理に基づいた体系的なアルゴリズムが使われるため，案外複雑なものとなる．

例えば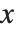， についての多項式を因数分解するには，まず，17のような素数を法として，その素数ともとの多項式を法とした 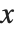の高次ベキで還元することにより得られた行列の零空間を求める．次に，各種の代数学と解析学の定理を使い，同じ素数の連続するベキを法として「持上げ」操作が行われることで整数係数上における因数分解が完了する．

このように，体系化した強力なアルゴリズムが使われているので，組込み関数だけを使い，難解な式でも，一般化された式でもすべてを一様に扱うことができる．しかし，式が単純なものなら，わざわざ複雑な処理をしなくてもよく，事実，単純な計算には，より効率の高い簡素化されたアルゴリズムが使われるようにもなっている．

このように，特殊ケースにも対応しているため，組込み関数には数多くの補助的なコードが付加されている．このために，カーネル全体のコード形態が非常に複雑なものになってしまっている．ちなみに，関数によっては基本的なソースコードだけなら5ページの記述で済むところが，補助的なコードのため100ページの長さになってしまったものもある．

Wolfram言語で使われるアルゴリズムは，上記の特殊なものも入れて，ほとんどが手作業で構築されたものであるが，中にはコンピュータを使い自動的に生成されたものもある．

このようなものに，機械精度による数学関数の評価で使われる数値解析アルゴリズムがある．アルゴリズムの主要な部分はなるべくコンパクトで，かつ，最高精度の近似をもたらす式からなっている．

数値解析に使われる式の多くは，Wolfram言語を使い導出されたものである．最終的な式の構築のために，非常に長いコンピュータ時間が費やされるが，その結果として，関数を効率よく評価できる短く最適化された式が得られている．

Wolframシステムは，今日までに開発されたソフトウェアシステムの中で最も複雑なものの一つだろう．これはC/C++，Java，Wolfram言語の各言語で書かれた数百万行のソースコードから構築されている．

WolframシステムのC言語コードは，特殊なメモリ管理およびオブジェクト指向の機能を備えたカスタマイズされたC言語で記述されている．また，Wolfram言語のコードは，ShareとDumpSaveの機能が使われ最適化が図られている．

Wolfram言語カーネルを構成している各コード部の比率は次の通りである．言語処理とシステム機能30%，数値解析機能20%，記号代数機能20%，そして，グラフィックスとカーネル出力機能に30%のコード量が使われている．

コードのほとんどはアルゴリズムを記述したもので，非常に緻密なものである．中には単純な手続きやテーブルの参照操作をもとにしたコードもあるが，それらは主に高レベルのWolfram言語で直接記述されている．

1パーセントに満たない小さな部分を除き，カーネルのソースコードはコンピュータシステムに依存しない形で記述されている．

しかし，フロントエンドはそうはいかない．各コンピュータシステムに適したユーザインターフェース環境を提供しなければいけない．このため，コンピュータシステムごとに特別なコードが必要になる．フロントエンドのソースコードはC++ 言語で書かれており，その規模は，約70万行におよび，内20万行は式の表示に関するものである．また，5万〜10万行のコードはユーザインターフェースの環境を提供するためにある．

Wolframシステムはクライアント・サーバ形式の計算環境も提供している．具体的には，外部プログラムとの連結を行う Wolfram Symbolic Transfer Protocol (WSTP)を介すことによって，フロントエンドとカーネルの接続を達成している．WSTPはTCP/IPを基盤とするものや共有メモリを使ったものを含め，複数のトランスポート層をサポートする．

フロントエンドとカーネルは3つの独立したWSTP接続を介して接続される．1つはユーザが開始する評価に使われる．2つ目はフロントエンドでDynamic式の値を解くために使われる．3つ目はカーネルがフロントエンドに，無効にしなければならないDynamicオブジェクトを知らせるために使われる．

Wolfram言語カーネルのCコード部分は一体性と一貫性を兼ね備えている．これらの機能は，カーネルの各部分における別の部分との相互通信を，Wolframシステムの式の交換を行うということを基本にすることで達成している．

このように，ソースコードのレベルでWolframシステムは機能別に独立したモジュール構成になっている．構成上は独立しているが，処理上は，モジュール間で関数の呼出し合いが行われるため相互依存の形を取っている．事実，数値解析的な関数が代数計算アルゴリズムを呼び出したり，グラフィックス関連のコードで，一見全く関連がないような数学アルゴリズムが使われたりすることがよくある．

1986年に開発が始まって以来，Wolframシステムのコーディング作業に費やされた労力は，ほぼ約千人の開発者が1年間通しで費やす時間に匹敵する．さらに，プログラムのテストや動作確認にもそれ以上の労力が注ぎ込まれている．

Wolframシステムのバージョンが更新されるにつれ，コードの内容は大きく変貌している．カーネルのコードは，バージョン1で15万行だったのが，バージョン2では35万行になり，さらに，バージョン3では60万行，バージョン4では80万行，バージョン5では約150万行，バージョン6では250万行の大きさになっている．これまでの更新作業で加えられた変更により，バージョン6のコードはバージョン1とは似ても似つかないものになっている．後者が前者に占める割合は，数パーセントにしか満たない．

コードの詳細は変わっても，ユーザインターフェースの設計指針はいずれのバージョンでも変わってはいない．機能面においていろいろ強化されはしたが，Wolframシステムバージョン1で作成したプログラムは，そのほとんどが何も変更なしにバージョン6でも実行することができる．

Wolframシステムの品質管理の一環として，いずれのバージョンにおいても，各機能について長期に渡り厳重な検査が行われる．検査作業のほとんどはWolfram言語で書かれた自動検査システムを使い実施される．

自動検査システムにより，数百万に及ぶ入力がWolframシステムに与えられ，また，返ってくる出力が正確なものかどうか自動的に検査される．ただし，計算させる式や処理する命令によっては微妙な問題を含むため，自動判定が不可能なことがあり，そのようなときは検査結果を見直す必要が出てくる．例えば，擬似乱数発生アルゴリズムは毎回違う結果を当然出してくる．また，機械精度で演算をするとき，コンピュータの機種が変わると結果が微妙にずれることもある．このため，判定作業は，このような違いをどう吸収するかという難しい問題を含んでいる．

自動システムにおいて，検査に使われる入力は次の種類のものがある．

検査過程において，計算の答のみならず補助的な情報である出力メッセージや使ったメモリ量や計算スピードも自動システムでチェックされる．

さらに，特別仕様のバージョンのWolframシステムが作られ，プログラム内部で処理的に矛盾がないか入念に検査がなされる．この特別バージョンは製品バージョンに比べ数割の処理スピードでしか動かないが，その代り，計算処理のひとつひとつのステップにおいてメモリ状態に矛盾がないかや，割り込みが可能かどうか計算状態の詳細なチェックをしてくれる．

特別バージョンでは，さらに，コードのどの部分がアクセスされたか逐一記録されるので，内部関数の検査漏れがないかも確認できる仕組みになっている．

コンピュータシステムへの依存がないように，Wolframシステムの現行バージョンは，それがサポートされるすべてのコンピュータシステムでルーチン的な検査を受ける．システムのスピードにもよるが，この作業は，通常，数時間から数日のコンピュータ時間がかかる．

大掛かりな検査を繰り返しても，Wolframシステム自体の複雑さも手伝い，完全にエラーを根絶することは至難である．

Wolframシステムの正確さは非常に高く，その正確性は，よく知られる数学問題の証明より数段上をいくものである．それでも，一般に，非常に長い証明問題で何年も間違いが見付けられないことがあるように，Wolframシステムのような非常に複雑なソフトウェアでは，誤りがあったとしても，なかなか発見されない場合もある．

誤りが残ったとしても，十分な検査をこなしているので，ユーザがWolframシステムを使っていて，実際にそれを見付ける確率は非常に小さい．

計算をしていて予期しないエラーが発生したり，期待していなかった答が返されてきたときは，Wolframシステム自体の内部コードを問題にする前に，入力間違いやWolframシステムの機能の解釈間違いがないかどうかを確認してほしい．

確認後もWolframシステムの誤動作が続くようなら，今後のバージョンで誤作動が解決されるようにWolfram Researchのテクニカルサポート部まで連絡していただきたい．