This information is part of the Modelica Standard Library maintained by the Modelica Association.

Define specialized class function

Examples

function si
  input Real x;
  output Real y;
algorithm
  y = if abs(x) < Modelica.Constants.eps then 1 else Modelica.Math.sin(x)/x;
end si;

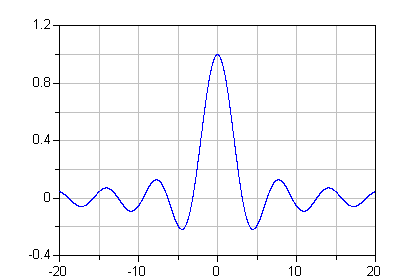
Syntax

   [ encapsulated ][ partial] [ pure | impure] function
   IDENT class_specifier

class_specifier :
   string_comment composition end IDENT
   | "=" base_prefix name [ array_subscripts ] [ class_modification ] comment
   | "=" enumeration "(" ( [enum_list] | ":" ) ")" comment

See Modelica Grammar for further details.

Description

The keyword function is used to define functions as known from programming languages.

The syntax and semantics of a function have many similarities to those of the block specialized class. A function has many of the properties of a general class, e.g., being able to inherit other functions, or to redeclare or modify elements of a function declaration.

Modelica functions have the following restrictions compared to a general Modelica class:

• Each input formal parameter of the function must be prefixed by the keyword input, and each result formal parameter by the keyword output. All public variables are formal parameters.
• Input formal parameters are read-only after being bound to the actual arguments or default values, i.e., they may not be assigned values in the body of the function.
• A function may not be used in connections, may not have equations, may not have initial algorithms.
• A function can have at most one algorithm section or one external function interface (not both), which, if present, is the body of the function.
• For a function to be called in a simulation model, the function may not be partial, and the output variables must be assigned inside the function either in declaration assignments or in an algorithm section, or have an external function interface as its body, or be defined as a function partial derivative. The output variables of a function should be computed.
• A function cannot contain calls to the Modelica built-in operators der, initial, terminal, sample, pre, edge, change, reinit, delay, cardinality, inStream, actualStream, to the operators of the built-in package Connections, and is not allowed to contain when-statements.
• The dimension sizes not declared with (:) of each array result or array local variable [i.e., a non-input components] of a function must be either given by the input formal parameters, or given by constant or parameter expressions, or by expressions containing combinations of those. If an output or a local array dimension is declared with (:), the size of the dimension can be changed in the function. A size change takes place by assigning a full array with the respective sizes to the dynamically sized array on the left hand side of an equal sign.
• The local variables of a function are not automatically initialized to the implicit default values of the data type [(e.g., 0.0 for Real) for performance reasons. It is the responsibility of the user to provide explicit defaults or to define the values of such variables before they are referenced.]
• Components of a function will inside the function behave as though they had discrete-time variability.

Modelica functions have the following enhancements compared to a general Modelica class:

• A function may be called using a mix of positional (as in conventional programming languages) and named arguments.
• A function can be recursive.
• A formal parameter or local variable may be initialized through a binding (=) of a default value in its declaration. Initialization through an equation is not possible.
• A function is dynamically instantiated when it is called rather than being statically instantiated by an instance declaration, which is the case for other kinds of classes.
• A function may have an external function interface specifier as its body.
• A function may have a return statement in its algorithm section body.
• A function allows dimension sizes declared with (:) to be resized for non-input array variables (so the actual dimension need not to be known when the function is translated).

A function may have a function as an input argument. The declared type of such an input formal parameter in a function can be the class-name of a partial function that has no replaceable elements. It cannot be the class-name of a record [i.e., record constructor functions are not allowed in this context.] Such an input formal parameter of function type can also have an optional functional default value. Example:

function quadrature "Integrate function y=integrand(x) from x1 to x2"
  input  Real x1;
  input  Real x2;
  input  Integrand integrand;   // Integrand is a partial function, see below
  // With default: input Integrand integrand := Modelica.Math.sin;
  output Real integral;
algorithm
  integral :=(x2-x1)*(integrand(x1) + integrand(x2))/2;
end quadrature;

partial function Integrand
  input  Real x;
  output Real y;
end Integrand;

A functional argument can be provided in one of the following forms to be passed to a formal parameter of function type in a function call (see examples below):

1. as a function name,
2. as a function partial application,
3. as a function that is a component,
4. as a function partial application of a function that is a component.

In all cases the provided function must be "function type compatible" to the corresponding formal parameter of function type. Example:

// A function as a positional input argument according to case (a)
function Parabola
   extends Integrand;
algorithm
   y = x*x;
end Parabola;

area = quadrature(0, 1, Parabola);

// The quadrature2 example below uses a function integrand that
// is a component as input argument according to case (c):
function quadrature2 "Integrate function y=integrand(x) from x1 to x2"
  input  Real x1;
  input  Real x2;
  input  Integrand integrand;   // Integrand is a partial function type
  output Real integral;
algorithm
   integral := quadrature(x1,       (x1+x2)/2, integrand)+
               quadrature((x1+x2)/2, x2,       integrand);
end quadrature2;