Fit
 Fit[data, funs, vars] finds a least-squares fit to a list of data as a linear combination of the functions funs of variables vars.
Fit[data, funs, vars] finds a least-squares fit to a list of data as a linear combination of the functions funs of variables vars.
 The data can have the form
The data can have the form 
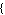
 ,
,  , ... ,
, ... , 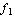
 ,
, 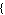
 ,
,  , ... ,
, ... , 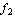
 , ...
, ...  , where the number of coordinates x, y, ... is equal to the number of variables in the list vars.
, where the number of coordinates x, y, ... is equal to the number of variables in the list vars.
 The data can also be of the form
The data can also be of the form 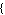
 ,
,  , ...
, ...  , with a single coordinate assumed to take values 1, 2, ... .
, with a single coordinate assumed to take values 1, 2, ... .
 The argument funs can be any list of functions that depend only on the objects vars.
The argument funs can be any list of functions that depend only on the objects vars.
 Fit[
Fit[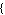
 ,
,  , ...
, ...  ,
,  1, x, x^2
1, x, x^2 , x] gives a quadratic fit to a sequence of values
, x] gives a quadratic fit to a sequence of values  . The result is of the form
. The result is of the form  +
+  x +
x +  x^2, where the
x^2, where the  are real numbers. The successive values of x needed to obtain the
are real numbers. The successive values of x needed to obtain the  are assumed to be 1, 2, ... .
are assumed to be 1, 2, ... .
 Fit[
Fit[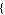
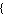
 ,
, 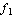
 ,
, 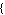
 ,
, 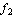
 , ...
, ...  ,
,  1, x, x^2
1, x, x^2 , x] does a quadratic fit, assuming a sequence of x values
, x] does a quadratic fit, assuming a sequence of x values  .
.
 Fit[
Fit[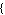
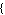
 ,
,  ,
, 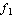
 , ...
, ...  ,
,  1, x, y
1, x, y ,
,  x, y
x, y ] finds a fit of the form
] finds a fit of the form  +
+  x +
x +  y.
y.
 Fit always finds the linear combination of the functions in the list forms that minimizes the sum of the squares of deviations from the values
Fit always finds the linear combination of the functions in the list forms that minimizes the sum of the squares of deviations from the values  .
.
 Exact numbers given as input to Fit are converted to approximate numbers with machine precision.
Exact numbers given as input to Fit are converted to approximate numbers with machine precision.
 See The Mathematica Book on the web: Section 1.6.6 and Section 3.8.1.
See The Mathematica Book on the web: Section 1.6.6 and Section 3.8.1.
 Implementation Notes: see Section A.9.4.
Implementation Notes: see Section A.9.4.
 See also: Interpolation, InterpolatingPolynomial, Solve, FindMinimum.
See also: Interpolation, InterpolatingPolynomial, Solve, FindMinimum.
Further Examples