ParallelAxis
2D/3D• ParallelAxis[vec, mass, inertia] uses the parallel axes theorem to transform the inertia properties of a body into or out of a centroidal reference frame. Assuming that the given inertia properties are centroidal, ParallelAxis returns the inertia properties relative to a noncentroidal reference frame in which vec is the vector from the origin of the noncentroidal frame to the centroid of the body. • The sign of the specified vector pointing to the centroid of the body is irrelevant.
• In Modeler2D, inertia is specified by a scalar and the return value is a scalar.
• In Modeler2D, simply negate mass to transform noncentroidal properties into a centroidal reference frame.
• In Modeler3D, the inertia of the body is specified by a list of the elements of the inertia matrix: {Ixx, Iyy, Izz, Ixy, Iyz, Izx} or a full inertia matrix. ParallelAxis then returns the list {Ixx', Iyy', ... } of inertia properties relative to the noncentroidal reference frame.
• In Modeler3D, ParallelAxis[centroid, mass, inertia, rotation] is used to specify that the centroidal reference frame in which the specified inertia properties are calculated is rotated relative to the noncentroidal frame. The rotation of the centroidal frame is specified by {angle, axis}, a virtual rotation vector, or a set of Euler parameters.
• In Modeler3D, to transform noncentroidal inertia properties into a centroidal reference frame: vec is the vector (in the centroidal reference frame) from the centroid to the origin of the noncentroidal reference frame, rotation specifies the relative rotation (in the centroidal reference frame) of the noncentroidal frame, and a negative mass is specified.
• See also: CompositeInertia, GyroFilter, PrincipalAxes. Further Examples Load the Modeler3D package. Here are inertia properties transformed from a noncentroidal to centroidal reference frame.
Out[2]= | 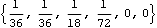 |
Here are the principal axes of the resulting inertia properties.
Out[3]= | 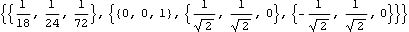 |
This rotates the original inertia matrix into the principal frame.
Out[4]= | 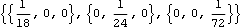 |
Here is the result of combining two sets of inertia properties.
Out[5]= | 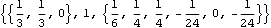 |
|