This approach to the design of controllers for multivariable systems is based on extending the concept of eigenvalues and eigenvectors of a square matrix of constants to those of a rational matrix. In the context of control system design, the latter eigenvalues and eigenvectors are often called the characteristic values and characteristic-direction vectors, respectively. Consider a system described by a p × p transfer-function matrix G(s). Associated with G(s) is the characteristic equation where g is a complex variable and where, in general, the function  (g, s) can be factored into a product of polynomials i(g,s) in g, i = 1, ..., p, which are irreducible over the field of rational functions, that is, In other words, G(s) has characteristic values that are functions of a complex variable. Hence, letting s trace out the Nyquist D-contour in the complex plane, and computing the corresponding characteristic values, enables a set of curves to be generated in the complex plane. This procedure essentially generates a set of generalized Nyquist diagrams, or characteristic loci (Postlethwaite and MacFarlane (1979)). The primary importance of these characteristic loci is that they enable the Nyquist stability criteria for single-input, single-output systems to be generalized to the multivariable case. Figure 5.2 shows a standard multivariable system feedback configuration where G(s), K(s), and F(s) represent the plant, controller, and negative feedback connections, respectively. If po is the number of right half-plane poles for the open-loop system, then closed-loop stability requires that the net sum of critical point {-1, 0} encirclements of the characteristic loci of G(s)K(s)F(s), or F(s)G(s)K(s), or K(s)F(s)G(s), be counterclockwise and equal in number to po. These different loop-gain matrices correspond to different loop break points, that is, the matrix product FGK corresponds to breaking the feedback loops in the error channel, the matrix product KFG corresponds to breaking the loops at the plant inputs, and GKF corresponds to breaking the loops at the feedback compensator inputs.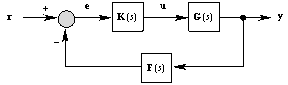 
Figure 5.2. Standard multivariable system feedback configuration. Let Q(s) = G(s)K(s) be the p × p open-loop transfer-function matrix of the standard multivariable feedback configuration with unity feedback. Suppose Q(s) has a set of characteristic values, and suppose that the set of associated eigenvectors {wi(s)} are a basis for the p-dimensional complex space for all values of s on a specified contour 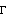 . Then, by definition, where wi(s) is the characteristic-direction vector corresponding to the characteristic value qi(s). The matrices W(s) and V(s) are defined as respectively having columns and rows that are the characteristic-direction vectors and reciprocal characteristic-direction vectors of Q(s). For non-oscillatory behavior each locus must avoid the region of the critical point and, for good steady-state accuracy, the characteristic loci must have large modulus at low frequencies. Such a condition would simultaneously ensure the reduction of low-frequency interaction. For reduced interaction at high frequencies, large loci cannot be relied upon and therefore at such frequencies the alignment of the characteristic-direction vectors with the standard basis vectors must be improved. When feedback is applied to the system with F(s) = Ip, the characteristic-direction vector set {wi(s), i = 1, 2, ..., p} is the same for both the open-loop and closed-loop systems Q(s) and H(s), respectively. For small amounts of closed-loop interaction, only the ith output of H(s) must respond to the ith input. This, in turn, simply means that either the characteristic gains are almost equal or that one of the standard basis vectors ei, where 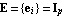 must be a characteristic-direction vector of H(s), and therefore of Q(s). It then follows that a sufficient condition for a small amount of high-frequency interaction is that the characteristic direction set of Q(s) must approach the standard basis vectors at high frequencies. A measure of the high-frequency alignment of the characteristic-direction vectors with the Euclidean-basis set is the closeness of the singular values of the system at the high frequencies concerned. In order to achieve these requirements, the method breaks the frequency range of interest into three regions, namely low, intermediate, and high, and deals with each separately. First, in the high-frequency region, a real controller Kh is designed for the improvement (that is, reduction) of the misalignment angles between the characteristic-direction vectors of G(j ) and the standard basis vectors ei. The resulting forward-path transfer-function matrix G1(s)=G(s)Kh is then considered as the new plant transfer-function matrix. Next, at intermediate frequencies, two real matrices Wm and Vm are computed as approximations of the matrix of complex characteristic-direction vectors and matrix of reciprocal characteristic-direction vectors of G1(s), respectively. The intermediate-frequency controller is then synthesized as 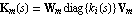 where each ki(s), for i = 1, 2, ..., p, is a single-input, single-output controller that would phase compensate (about the critical point) the scalar plant whose frequency plot is given by the ith characteristic transfer function of G1(s). This controller is known as the "approximate commutative controller" (Kouvaritakis (1974)). Additionally, the intermediate-frequency controller must tend to the unity matrix at high frequencies, so that it does not upset the characteristic-direction vector alignment affected in the first stage of the design. This procedure results in the new plant, with the forward-path transfer-function matrix In the final stage of the design, two real matrices W and V are computed to approximate the matrix of characteristic-direction vectors and matrix of reciprocal characteristic-direction vectors of G2(s), respectively, at low frequencies. The low-frequency controller is then assembled in accordance with the equation where each scalar gain ki, for i = 1, 2, ..., p, is intended to adjust in magnitude the ith characteristic transfer function of G2(s) at low frequencies, and  determines the duration of the integral action as increases. Thus, K(s) at low frequencies will introduce integral action (injecting high gains into the system) as well as balance up the magnitudes of the characteristic loci. At higher frequencies, the 1/s term will become negligibly small so that K (s) will tend to the identity operation. |
