WishartDistribution[Σ,m]
represents a Wishart distribution with scale matrix Σ and degrees of freedom parameter m.


WishartDistribution
WishartDistribution[Σ,m]
represents a Wishart distribution with scale matrix Σ and degrees of freedom parameter m.
Details and Options
- To use WishartDistribution, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
- The probability density for a symmetric positive definite matrix
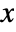 in a Wishart distribution is proportional to
in a Wishart distribution is proportional to 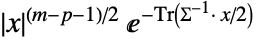 .
. - The scale matrix Σ can be any symmetric positive definite matrix. The parameter m can be any number such that m>Length[Σ].
- For integer m, the Wishart distribution gives the distribution of covariance matrices of multinormal samples.
- WishartDistribution can be used with such functions as Mean, PDF, and RandomReal.
Examples
open all close allPossible Issues (2)
WishartDistribution is not defined when Σ is not symmetric and positive definite:
WishartDistribution is not defined when m<Length[Σ]:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Related Guides
Text
Wolfram Research (2007), WishartDistribution, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html.
CMS
Wolfram Language. 2007. "WishartDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html.
APA
Wolfram Language. (2007). WishartDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html
BibTeX
@misc{reference.wolfram_2025_wishartdistribution, author="Wolfram Research", title="{WishartDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html}", note=[Accessed: 02-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_wishartdistribution, organization={Wolfram Research}, title={WishartDistribution}, year={2007}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html}, note=[Accessed: 02-January-2026]}