Notation, Symbolize, and InfixNotation

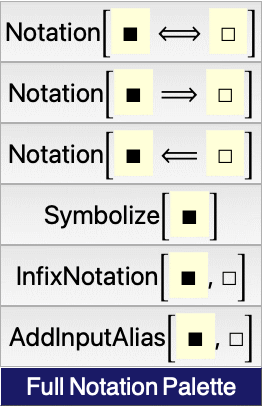
NotationInfixNotation
SymbolizeEntering Notations

Notation

Notation[boxes ⟺ expr]set boxes to be parsed to expr and expr to be formatted as boxes
Notation[boxes ⟹ expr]set boxes to be parsed to expr
Notation[boxes ⟸ expr]set expr to be formatted as boxes
Notation[notation, opts]define a notation notation with the options opts
RemoveNotation[notation]remove the notation notation

Syntax of notation declarations.

Notation takes both an external representation and an internal representation as arguments. The Wolfram Language translates any input matching the external representation into the corresponding internal representation and, reciprocally, formats any expression matching the internal representation into the corresponding external representation. In this context, representation means a composite structure made up of boxes representing some "notation".

This loads the package.
The following declares a new notation for gplus.
Any input matching x_ ⊕n_ y_ is now interpreted as gplus[x,y,n].
Any gplus expression is now formatted in the new notation.

Notations defined using ⟺ in their definition both parse and format expressions according to the given notation. However, you can restrict the notation to only parsing or only formatting by using ⟹ or ⟸ respectively, instead of ⟺ in your notation statements.

This defines a notation for the parsing of a hypothetical DomainIntegral.
DomainIntegral is now parsable.
The following defines an output format for Derivative objects that looks more like that of traditional mathematics.
Derivatives are now formatted according to the new derivative notation.
To allow the previous output to be used as input, you can define an interpretation of partial derivatives.
You can now use these new notations for derivatives.

You should define your notations in such a way that they both parse and format, since users will generally expect this functionality.

The following notation both formats and parses arrows overscripted by Apply.
Simple rules like linearity can now be entered in a visually intuitive way.

You may at first feel that having underscores on both sides of a Notation statement is somewhat unsettling. However, notational transformations usually work in both directions, therefore having underscores on both sides of a notation statement is natural, and soon becomes intuitive.

Symbolize

Symbolize[boxes]treat boxes as a symbol
Symbolize[boxes,opts]treat boxes as a symbol with the options opts
RemoveSymbolize[boxes]remove the treatment of boxes as a symbol

Syntax of symbolization declarations.

Symbolize is used to treat a class of composite boxes internally as symbols. It is sometimes necessary and desirable to be able to symbolize composite objects; for example, to be able to attach rules to a composite object, it must be treated as a symbol.

This declares that the composite object ℴ∂ should be treated as a symbol.
The package has created a FullForm name for the composite symbol ℴ∂.
You can now attach rules to the composite symbol ℴ∂.
The above rule for ℴ∂ is now tried before the rules of DomainIntegral.
Symbolize also symbolizes classes of expressions, for example, to symbolize all objects subscripted by Rule.
Anything subscripted by Rule is now treated as a symbol.

You can use symbolized box structures as pattern variables in definitions. This lets you create formulas in a more familiar notation. However, you must use pattern expressions of the form CompositePatternVariable: PatternContent otherwise the Wolfram Language may interpret the pattern expression as CompositePatternVariable * PatternContent.

This defines the transmission coefficient for an incident wave packet on a potential step under certain conditions.

InfixNotation

InfixNotation[op,func]treat op as an infix operator representing the function func
InfixNotation[op,func,opts]treat op as an infix operator representing the function func with the options opts
RemoveInfixNotation[op,func]remove the composite infix operator op

Syntax of infix notation declarations.

InfixNotation is used to treat a composite box structure as an infix operator. InfixNotation requires both a composite box object that will represent the infix operator and a symbol that will be the full form head of the expression. A simple parallel of this duality in the Wolfram Language is that the infix notation + has the full form head Plus.

This declares that the composite object +{} should act as the infix form of Join.
The infix notation +{} both parses input and formats output.

An advantage of using InfixNotation over that of using Notation to define an infix operator is that InfixNotation parses an expression into a flat internal form without evaluation. Although this is a subtle difference, it is an important one (see ring operations and parsing without evaluation.)

InfixNotation parses input to a flat expression.

The function InfixNotation can be compared to using the infix form of functions ~f~ (compare to "Special Ways to Input Expressions").

Entering Notations

When defining your own notations it is critically important to use the notation templates. The notation templates are contained in the notation palette shown below.

1.gif

The reason for this restriction is that the templates pasted into a notebook contain essential tag boxes embedded in the correct way. These embedded tag boxes allow Notation , Symbolize, and InfixNotation to properly group and parse the new notation being defined. Further, they allow these functions to get the styling information of the new notation so that the output is formatted with the same spacing, sizes, adjustments, etc. as the input.

A blank notation template looks like the following.

Advanced note: you can circumvent using the notation palette by wrapping the corresponding literal box structures in a ParsedBoxWrapper.

In the Wolfram Language, it is possible to create input aliases for any notation or expression you want. The normal interface to these input aliases is rather cumbersome and so the notation package contains the function AddInputAlias to facilitate adding input aliases to the current notebook. Each of the common templates has an alias associated with it for easy entry. For instance, typing Esc notation Esc in an input cell will enter the notation template Notation[ ⟺ ].

Add an input alias for apply statements to the current notebook.

Now that we have created this alias, we can enter "apply" templates by simply typing Esc apply Esc.