AcyclicGraphQ
Background & Context
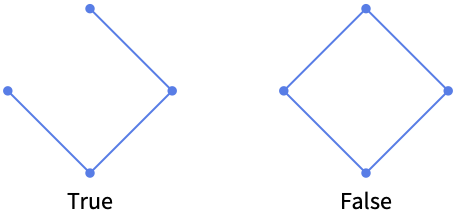
- AcyclicGraphQ checks if a graph is cycle-less. A graph cycle (more properly called a circuit when the cycle is identified using an explicit path with specific endpoints) is a subset of a graph's edge set that forms a connected path such that the first node of the path corresponds to the last. A graph with no cycles is known as an acyclic graph, while a graph containing one or more cycles is called a cyclic graph. AcyclicGraphQ returns True for an acyclic graph (ignoring any self-loops) and False otherwise.
- A simple graph containing no cycles of length three is called a triangle-free graph, and a simple graph containing no cycles of length four is called a square-free graph. Simple acyclic graphs are therefore triangle-free and square-free. They are also non-Hamiltonian (i.e. they contain no Hamiltonian cycles).
- A connected acyclic graph is known as a tree. All trees are therefore acyclic by definition, and TreeGraphQ (which is equivalent to the logical conjunction of AcyclicGraphQ and ConnectedGraphQ) can be used to check if a graph is a tree. Trees appear extensively in computer science and in particular in the implementation of many types of algorithms and data structures, including file and folder storage on disk.
- A not-necessarily-connected acyclic graph is known as a forest. A forest with directed edges is more commonly known as a directed acyclic graph or DAG. A DAG is therefore a graph for which both AcyclicGraphQ and DirectedGraphQ return True. DAGs are important in modeling many different kinds of information, e.g. electronic circuits, information flows, and events and tasks.
- FindCycle can be used to find one or more cycles in graphs that are not acyclic (and returns the empty list {} for graphs that are).
Examples
open all close allScope (6)
AcyclicGraphQ works with undirected graphs:
AcyclicGraphQ gives False for expressions that are not graphs:
AcyclicGraphQ works with large graphs:
Applications (1)
Properties & Relations (6)
Use DepthFirstScan to detect cycles in a graph:
Compare with AcyclicGraphQ:
A CycleGraph is not acyclic:
A TreeGraph is acyclic:
A PathGraph with different start and end vertices is acyclic:
An acyclic graph is not Hamiltonian:
A graph with minimal vertex degree greater than 2 is not acyclic:
Possible Issues (1)
AcyclicGraphQ ignores self-loops:
Related Guides
History
Text
Wolfram Research (2010), AcyclicGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.
CMS
Wolfram Language. 2010. "AcyclicGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.
APA
Wolfram Language. (2010). AcyclicGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcyclicGraphQ.html
BibTeX
@misc{reference.wolfram_2025_acyclicgraphq, author="Wolfram Research", title="{AcyclicGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AcyclicGraphQ.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_acyclicgraphq, organization={Wolfram Research}, title={AcyclicGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/AcyclicGraphQ.html}, note=[Accessed: 05-January-2026]}