BernoulliB[n]
gives the Bernoulli number ![]() .
.
BernoulliB[n,x]
gives the Bernoulli polynomial ![]() .
.


BernoulliB
BernoulliB[n]
gives the Bernoulli number ![]() .
.
BernoulliB[n,x]
gives the Bernoulli polynomial ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- The Bernoulli polynomials satisfy the generating function relation
 te^(xt)/(e^t-1)=sum_(n=0)^(infty)TemplateBox[{n, x}, BernoulliB2](t^n/n!)](Files/BernoulliB.en/3.png) .
. - The Bernoulli numbers are given by
![TemplateBox[{n}, BernoulliB]=TemplateBox[{n, 0}, BernoulliB2] TemplateBox[{n}, BernoulliB]=TemplateBox[{n, 0}, BernoulliB2]](Files/BernoulliB.en/4.png) .
. - For odd
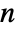 , the Bernoulli numbers are equal to 0, except
, the Bernoulli numbers are equal to 0, except ![TemplateBox[{1}, BernoulliB]=-1/2 TemplateBox[{1}, BernoulliB]=-1/2](Files/BernoulliB.en/6.png) .
. - BernoulliB can be evaluated to arbitrary numerical precision.
- BernoulliB automatically threads over lists.
Examples
open all close allScope (3)
Applications (6)
Find sums of powers ![]() using BernoulliB (Faulhaber's formula):
using BernoulliB (Faulhaber's formula):
Compare with direct summation:
Set up an Euler–Maclaurin integration formula:
Compare with the exact summation result:
Plot roots of Bernoulli polynomials in the complex plane:
Show the approach of Bernoulli numbers to a limiting form:
The denominator of Bernoulli numbers is given by the von Staudt–Clausen formula:
Compute Bernoulli numbers in modular arithmetic modulo a prime:
Properties & Relations (3)
Find BernoulliB numbers from their generating function:
Find BernoulliB polynomials from their generating function:
BernoulliB can be represented as a DifferenceRoot:
Possible Issues (2)
Algorithmically produced results are frequently expressed using Zeta instead of BernoulliB:
When entered in the traditional form, ![]() is not automatically interpreted as a Bernoulli number:
is not automatically interpreted as a Bernoulli number:
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 2008 (7.0)
Text
Wolfram Research (1988), BernoulliB, Wolfram Language function, https://reference.wolfram.com/language/ref/BernoulliB.html (updated 2008).
CMS
Wolfram Language. 1988. "BernoulliB." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/BernoulliB.html.
APA
Wolfram Language. (1988). BernoulliB. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BernoulliB.html
BibTeX
@misc{reference.wolfram_2025_bernoullib, author="Wolfram Research", title="{BernoulliB}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BernoulliB.html}", note=[Accessed: 21-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_bernoullib, organization={Wolfram Research}, title={BernoulliB}, year={2008}, url={https://reference.wolfram.com/language/ref/BernoulliB.html}, note=[Accessed: 21-January-2026]}