ControllableModelQ[sys]
yields True if the state-space model sys is controllable, and False otherwise.
ControllableModelQ[{sys,sub}]
yields True if the subsystem sub is controllable.


ControllableModelQ
ControllableModelQ[sys]
yields True if the state-space model sys is controllable, and False otherwise.
ControllableModelQ[{sys,sub}]
yields True if the subsystem sub is controllable.
Details and Options

- ControllableModelQ is also known as a reachable model.
- A state-space model is said to be controllable if for any initial state
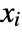 and any final state
and any final state 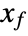 there exists some control input that drives the state from
there exists some control input that drives the state from 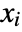 to
to 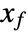 in finite time.
in finite time. - The system sys can be a standard or descriptor StateSpaceModel or AffineStateSpaceModel.
- The following subsystems sub can be specified: » »
-
All whole system "Fast" fast subsystem "Slow" slow subsystem {λ1,…} subsystem with eigenmodes 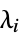
- The "Fast" and "Slow" subsystems primarily apply to descriptor state-space models as described in KroneckerModelDecomposition.
- The eigenmodes λi are described in JordanModelDecomposition.
- ControllableModelQ accepts a Method option with the following settings:
-
Automatic automatically choose the appropriate test "Distribution" use controllability distribution's rank "Gramian" use controllability Gramian's rank or positive definiteness "Matrix" use controllability matrix's rank "PBH" use Popov–Belevitch–Hautus rank test
Examples
open all close allBasic Examples (2)
Scope (6)
Test the controllability of a system with approximate coefficients:
Controllability is equivalent to controllability of both slow and fast modes (C-controllability):
Test controllability of individual eigenmodes:
The system is uncontrollable because of eigenmode ![]() :
:
This can be seen in the Jordan form, where there is no way to affect the third state:
Test controllability of an AffineStateSpaceModel:
If an operating point ![]() is given, controllability from
is given, controllability from ![]() is tested:
is tested:
Options (7)
Method (7)
By default, the controllability matrix is used for exact and symbolic systems:
The system is controllable if the ControllabilityMatrix has full rank:
The controllability Gramian is used for stable numeric systems:
The system is controllable if the ControllabilityGramian has full rank:
For the controllability Gramian, this is equivalent to it being positive definite:
The PBH rank test is used for all other numeric systems:
The system is controllable because ![]() has full rank for all
has full rank for all ![]() :
:
The controllability distribution is used for input-linear systems:
For linear systems, the tests based on the controllability matrix and distribution are equivalent:
Controllability of the linearized system implies controllability of the input-linear system:
The matrix test for input linear system uses the "Matrix" method for the linearized system:
Using no control input, the system follows the drift vector field ![]() :
:
A system is weakly controllable if the drift vector field can also be used to move state:
Without including the drift vector field, the system is not controllable:
Applications (5)
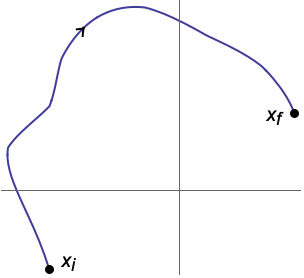
The position and velocities of all three masses can be controlled by the force on ![]() :
:
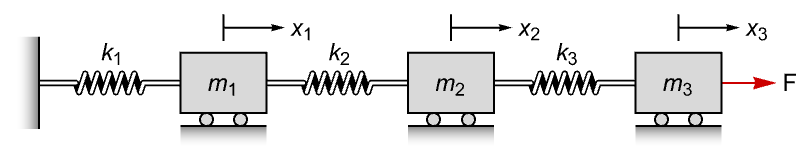
An electric circuit with the capacitor voltage and inductor current as states:
In general, the system is controllable:
However if ![]() , it is not controllable:
, it is not controllable:
A unicycle with drive and steering as input:
The system is controllable, but the linearized system is not:
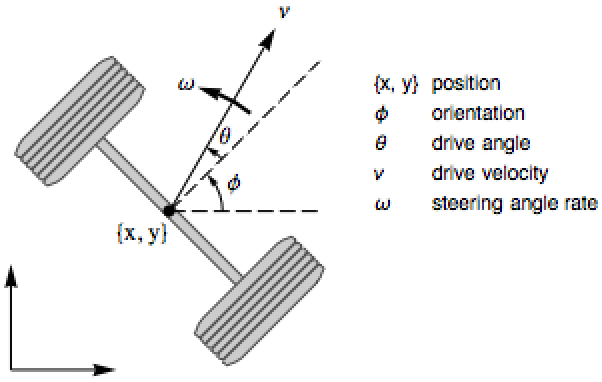
The system is controllable, but the linearized system is not:
A rotating rigid satellite modeled using Euler's equations of motion:
Its controllability for various values of the principal moments and actuator combinations:
If ![]() , the system is controllable with any two actuators:
, the system is controllable with any two actuators:
If ![]() , the system is not controllable with actuators 1 and 2 or any one actuator:
, the system is not controllable with actuators 1 and 2 or any one actuator:
Properties & Relations (7)
A diagonal system is controllable, assuming ![]() and
and ![]() :
:
With ![]() , there is no way to control the first state:
, there is no way to control the first state:
With ![]() , the first state cannot be controlled directly, but indirectly from the second state:
, the first state cannot be controlled directly, but indirectly from the second state:
With ![]() , the second state cannot be controlled directly or indirectly from the first state:
, the second state cannot be controlled directly or indirectly from the first state:
Use JordanModelDecomposition to compute the canonical state-space representation above:
Compute the controllability of each mode using the "PBH" test:
For descriptor systems, KroneckerModelDecomposition is the generalization of the diagonal form:
Determine the controllability of the slow subsystem from its structure:
Compute it using the original system:
Determine the controllability of the fast subsystem:
Compute it using the original system:
If the descriptor matrix of a StateSpaceModel has full rank, there is no fast subsystem:
Hence the complete controllability of the system can be evaluated from the slow subsystem:
Controllability is invariant under a nonsingular StateSpaceTransform:
Controllability is invariant under state feedback:
Compute the state feedback using StateFeedbackGains:
The closed-loop system is also controllable:
Controllability does not mean it is output controllable (OutputControllableModelQ):
Possible Issues (2)
The Gramian method is not reliable for systems that are not asymptotically stable:

The eigenvalue in the right half of the complex plane leads to instability for continuous-time systems:
For affine systems with nonzero drift, the distribution tests only for accessibility:
A random initial condition and random input signal generator:
Simulate the system 10 times with random inputs:
The system cannot be moved to the left of the initial point:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0)
Text
Wolfram Research (2010), ControllableModelQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllableModelQ.html (updated 2014).
CMS
Wolfram Language. 2010. "ControllableModelQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ControllableModelQ.html.
APA
Wolfram Language. (2010). ControllableModelQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ControllableModelQ.html
BibTeX
@misc{reference.wolfram_2025_controllablemodelq, author="Wolfram Research", title="{ControllableModelQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ControllableModelQ.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_controllablemodelq, organization={Wolfram Research}, title={ControllableModelQ}, year={2014}, url={https://reference.wolfram.com/language/ref/ControllableModelQ.html}, note=[Accessed: 06-March-2026]}