DiscreteMarkovProcess
DiscreteMarkovProcess[i0,m]
represents a discrete-time, finite-state Markov process with transition matrix m and initial state i0.
DiscreteMarkovProcess[p0,m]
represents a Markov process with initial state probability vector p0.
represents a Markov process with transition matrix from the graph g.
Details

- DiscreteMarkovProcess is also known as a discrete-time Markov chain.
- DiscreteMarkovProcess is a discrete-time and discrete-state random process.
- The states of DiscreteMarkovProcess are integers between 1 and
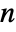 , where
, where 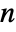 is the length of transition matrix m.
is the length of transition matrix m. - The transition matrix m specifies conditional transition probabilities m〚i,j〛Probability[x[k+1]jx[k]i], where x[k] is the state of the process at time k. »
- A discrete Markov process can be seen as a random walk on a graph, where the probability of transitioning from state
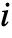 to state
to state 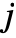 is specified by m〚i,j〛.
is specified by m〚i,j〛. - EstimatedProcess[data,DiscreteMarkovProcess[n]] indicates that a process with n states should be estimated.
- The transition matrix in the case of a graph g is constructed to give equal probability of transitioning to each incident vertex.
- DiscreteMarkovProcess allows m to be an
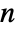 ×
×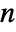 matrix with non-negative elements and rows that sum to 1, i0 is an integer between 1 and
matrix with non-negative elements and rows that sum to 1, i0 is an integer between 1 and 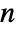 , and p0 is a vector of length
, and p0 is a vector of length 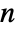 of non-negative elements that sum to 1.
of non-negative elements that sum to 1. - DiscreteMarkovProcess can be used with such functions as MarkovProcessProperties, PDF, Probability, and RandomFunction.
Examples
open allclose allBasic Examples (2)
Scope (14)
Estimate the process parameters from sample data:
Find the mean first passage time to state 3 starting in state 1:
Find the stationary distribution:
Visualize the process as a graph, with the transition probabilities given as tooltips:
Convert the graph representation back to a discrete Markov process:
Find the probability of eventual absorption into state 1 starting from state 4:
Define a discrete Markov process:
Find the communicating classes:
Find the recurrent and transient classes:
Find the first passage time mean and variance conditional on reaching the target states:
Calculate the probability of an event:
Calculate probability involving multiple time slices:
Assume that absorption occurs for the following process:
Calculate the probability of getting absorbed into state 3:
Calculate the probability of getting absorbed into state 4:
Moments and generating functions:
Visualize a simulation of the gambler's ruin process via the graph representation:
Generalizations & Extensions (2)
Applications (18)
Games (7)
Model the process of tossing a coin repeatedly, using a discrete Markov process where the probability of getting heads is 0.6 and getting tails is 0.4:
A biased coin with probability of getting heads being ![]() is flipped
is flipped ![]() times. Find the probability that the length of the longest run of heads exceeds a given number
times. Find the probability that the length of the longest run of heads exceeds a given number ![]() . This can be modeled by using a discrete Markov process, where the state
. This can be modeled by using a discrete Markov process, where the state ![]() represents having
represents having ![]() heads in a run. The resulting transition matrix for
heads in a run. The resulting transition matrix for ![]() ,
, ![]() , and
, and ![]() is given by:
is given by:
Simulate the number of heads in a run. If there is a run of 10 heads, the count is not restarted:
The probability of getting at least 10 heads in a run after 100 coin flips:
A gambler, starting with three chips, places a one-chip bet at each step, with a winning probability of 0.4 and a goal of winning seven units before going broke. The states here are the integers 1 through 8, representing the gambler's wealth plus one:
Find the expected number of times the gambler has ![]() units:
units:
Compare the above result to the one determined from a simulation:
Find the expected time until the gambler reaches his goal or goes broke:
Total states visited before the gambler reaches his goal or goes broke:
Verify the answer using simulation:
Find the probability of winning:
Find how many times, on average, you have to roll a die until you have seen all six faces:
Find the probability of seeing all the faces in ![]() rolls:
rolls:
Markov process for flipping the sequence THH with an unbiased coin:
Markov process for flipping the sequence HHH with an unbiased coin:
On average, it takes longer for HHH to occur than for THH:
In a game of tennis between two players, suppose the probability of the server winning a point is ![]() . There are 17 possible states:
. There are 17 possible states:
Visualize the random walk graph for ![]() :
:
Find the probability of the server winning the game if ![]() :
:
Find the mean time to absorption, that is, the number of points played:
Find the mean number of states visited:
Find the average number of times the score will be tied at deuce:
In the game of craps, a player rolls a pair of dice and sums the numbers. On the first throw, he wins if he rolls 7 or 11 and loses if he rolls 2, 3, or 12, while any other number is called a point and the dice rolls continue. In later throws, the player wins if he rolls the point number and loses if he rolls 7. The states are: start, win, lose, p4, p5, p6, p8, p9, or p10. He never returns to start, while win and lose are absorbing states. The following distribution represents a roll of two dice:
He wins on the first throw if he rolls 7 or 11:
He loses on the first throw if he rolls 2, 3, or 12:
He enters a "point" state on the first throw and continues playing if he rolls anything else:
Probability for losing starting from the point state:
The probability of staying in the same point state is:
The probability of losing is greater than the probability of winning:
Weather (3)
A simple weather model is: given that it rains today, it will rain tomorrow with probability 0.7; and given that it does not rain today, it will rain tomorrow with probability 0.4. Given that it is raining today, represent this model with a discrete Markov process and find the probability that it will rain four days from now. A representation of the weather:
The probability of rain in four days:
Build a weather model based on whether it rained on the two previous days. Suppose it will rain tomorrow with probability 0.7 if it rained today and yesterday, with probability 0.5 if it rained today but not yesterday, with probability 0.4 if it rained yesterday but not today, and with probability 0.2 if it did not rain yesterday or today. Use a product state space ![]() , where
, where ![]() indicates whether it rained yesterday and
indicates whether it rained yesterday and ![]() whether it rained today:
whether it rained today:
The remaining cases cannot happen:
The resulting transition probability matrix:
The resulting discrete Markov process:
The probability of rain in four days:
Find the long term probability of rain two days in a row:
Compare to a simulation over a long time period:
A taxi is located either at the airport or in the city. From the city, the next trip is to the airport with probability 1/4, or to somewhere else in the city with probability 3/4. From the airport, the next trip is always to the city. Model the taxi using a discrete Markov process with state 1 representing the city and state 2 representing the airport, starting at the airport:
Simulate a typical sequence of taxi runs:
Find the stationary distribution:
The stationary distribution indicates that the taxi spends ![]() of its time in the city:
of its time in the city:
Urns (1)
With ![]() balls distributed between urns A and B, at each step a ball is randomly selected and transferred to the other urn. Find the stationary distribution of balls in urn A. The count of balls in urn A can be modeled as a discrete Markov process. If there are
balls distributed between urns A and B, at each step a ball is randomly selected and transferred to the other urn. Find the stationary distribution of balls in urn A. The count of balls in urn A can be modeled as a discrete Markov process. If there are ![]() balls in urn A, the probability of losing a ball from A is
balls in urn A, the probability of losing a ball from A is ![]() , and the probability of gaining a ball is
, and the probability of gaining a ball is ![]() , which gives the transition matrix:
, which gives the transition matrix:
The stationary distribution for urn A:
The stationary distribution is the same, regardless of how the balls are initially distributed:
Random Walks (2)
Machine Repair (1)
A work cell in a machine shop consists of three machines, where on a given day a machine fails with probability 0.1. Machine 1 feeds both machines 2 and 3, and if machine 1 fails, there is no production that day. Only one machine can be repaired on the same day so it is available for the following day. If several machines are down, they are repaired in priority order 1, 2, and 3. A machine that has been repaired is assumed to be working the next day. Find the proportion of time there can be some production. The failure and repair process can be modeled as a discrete Markov process by enumerating all possible combinations of failed and working machines:
No machine down; one or several machines can fail the next day:
One machine down; it is repaired and one or both of the remaining ones can fail:
Two machines down; repairs are done in priority order and the remaining machines could fail:
All machines are down; machine 1 is repaired:
The resulting transition matrix:
The discrete Markov process, starting with all machines working:
There is production if no machines are down, or only one of machines 2 and 3 is down:
The probability that there is production at full capacity:
The average time it takes to get from all machines down to no machines down:
Insurance (1)
In a four-state Markov chain model of a Bonus–Malus auto insurance system, each policyholder is given one of the four states 1, 2, 3, or 4, depending on the number of claims made in the preceding year, and this state determines the annual premium. No claims typically results in a lower premium, while one or more claims typically result in a higher premium. With premium levels ![]() for the four states and the given transition matrix of a policyholder's successive states, find the average yearly premium if the policyholder's yearly number of claims is a Poisson random variable with mean
for the four states and the given transition matrix of a policyholder's successive states, find the average yearly premium if the policyholder's yearly number of claims is a Poisson random variable with mean ![]() :
:
Other (3)
Assuming there are 365 days in a year and each day is equally probable for a birthday, find the minimum number of people such that there is a 50% probability of at least two of them sharing a birthday. The states are ![]() —number of people having distinct birthdays
—number of people having distinct birthdays ![]() and
and ![]() —at least two people have the same birthday:
—at least two people have the same birthday:
Consider a simple natural selection model in which the population of a species on an isolated island is fixed at ![]() by the food supply. A mutant is born with a slightly better chance of survival than a regular member of the species, and in each generation the mutants either gain a place with probability
by the food supply. A mutant is born with a slightly better chance of survival than a regular member of the species, and in each generation the mutants either gain a place with probability ![]() or lose a place with probability
or lose a place with probability ![]() :
:
Probability of the mutants taking over the island:
Average number of generations required for the mutants to take over the island:
Suppose radio messages from Mars are written in a language that uses only one vowel A and four consonants BCDR, and interspersed in the ordinary communication are some long messages produced by a Markov chain with the following estimated transition matrix:
Find the mean distance between consecutive vowels:
Find the mean distance between consecutive consonants:
Find the mean and variance of the length of consecutive occurrences of B:
Text
Wolfram Research (2012), DiscreteMarkovProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html (updated 2014).
CMS
Wolfram Language. 2012. "DiscreteMarkovProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html.
APA
Wolfram Language. (2012). DiscreteMarkovProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html