FindVertexCover
finds a vertex cover of the graph g with a minimum number of vertices.
FindVertexCover[{vw,…}]
uses rules vw to specify the graph g.
Details

- FindVertexCover returns a list of vertices.
- FindVertexCover will return an empty list if no vertex cover is found.
- A vertex cover is a set of vertices that is incident to every edge.
- FindVertexCover works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.
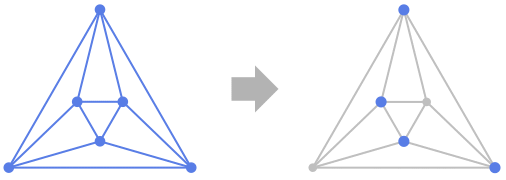
Background & Context
- FindVertexCover finds a single vertex cover of a graph, where a vertex cover is a subset of vertices satisfying the condition that each edge is incident to some vertex.
- FindVertexCover[g] finds a minimum vertex cover (i.e. a vertex cover of smallest possible size) of a graph g, while FindVertexCover[g,k] finds a vertex cover of size k. The size of a minimum vertex cover of a graph g is known as its vertex cover number. The problem of finding a minimum vertex cover (and hence the vertex cover number) of a general graph is NP-complete, meaning computation can be exponentially slow. However, a minimum vertex cover can be found in polynomial time for bipartite graphs (i.e. graphs whose vertex set can be partitioned into two independent sets).
- Vertex covers are closely related to independent vertex sets (which are sets of vertices such that no two belong to the same edge). In particular, a set of vertices is a vertex cover if and only if its complement forms an independent vertex set. The counts of vertex covers and independent vertex sets in a graph are therefore the same. Furthermore, the sum of the independence number (size of a maximum independent vertex) and the vertex cover number (size of a minimum vertex cover) of an undirected graph equals the vertex count.
- A vertex cover of a graph can be formed by taking the endpoints from each edge in a maximal independent edge set. (Here, an independent edge set is a set of edges such that no two member edges share a vertex. A maximal independent edge set is an independent edge set to which no other edge of the graph can be added without violating independence, while a maximum independent edge set is an independent edge set of maximum possible size for a given graph.) As a result, the size of a minimum vertex cover is always at most as large as twice the size of a maximum independent edge set. The König–Egerváry theorem states that for bipartite graphs, the size of a maximum independent edge set (i.e. the matching number) equals its vertex cover number.
- VertexCoverQ can be used to test if a given vertex set forms a vertex cover of a specified graph. A trivial implementation to find multiple vertex covers can therefore be written by applying VertexCoverQ to any desired subsets of a graph's vertices. Similarly, FindIndependentVertexSet can be used to find one or more maximal independent vertex sets in a graph, each of whose complements is a vertex cover. FindEdgeCover performs the analogous test to FindVertexCover for edge covers of a graph.
Examples
open allclose allScope (7)
FindVertexCover works with undirected graphs:
Use rules to specify the graph:
FindVertexCover works with large graphs:
Properties & Relations (6)
The result of FindVertexCover can be tested by VertexCoverQ:
A set of vertices is a vertex cover if its complement is an independent set:
Check that the complement set of vertices is independent:
The total size of the vertex cover and the largest independent set equals the vertex count:
The complement of the vertex cover in GraphComplement is a clique in its original graph:
Compute the complement using the same embedding:
The complete bipartite graph ![]() has vertex cover of size
has vertex cover of size ![]() :
:
The largest independent edge set in a bipartite graph has the same size as the smallest vertex cover:
Text
Wolfram Research (2010), FindVertexCover, Wolfram Language function, https://reference.wolfram.com/language/ref/FindVertexCover.html (updated 2015).
CMS
Wolfram Language. 2010. "FindVertexCover." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindVertexCover.html.
APA
Wolfram Language. (2010). FindVertexCover. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindVertexCover.html