Function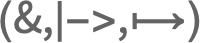

body& or Function[body]

is a pure (or "anonymous") function. The formal parameters are # (or #1), #2, etc.

x|->body or xbody or Function[x,body]

is a pure function with a single formal parameter x.

{x1,x2,…}|->body or {x1,x2,…}body or Function[{x1,x2,…},body]

is a pure function with a list of formal parameters.

Function[params,body,attrs]

is a pure function that is treated as having attributes attrs for purposes of evaluation.

Details

  • When Function[body] or body& is applied to a set of arguments, # (or #1) is replaced by the first argument, #2 by the second, and so on. #0 is replaced by the function itself.
  • If there are more arguments supplied than # i in the function, the remaining arguments are ignored. »
  • ## stands for the sequence of all arguments supplied. »
  • ## n stands for arguments from number n onward. »
  • When applied to an association, #name is equivalent to #["name"], and picks out elements in the association.
  • In the form #name, the characters in name can be any combination of alphanumeric characters not beginning with digits.
  • The character is entered as |->, fn or \[Function].
  • Function is analogous to λ in LISP or formal logic.
  • Function has attribute HoldAll. The function body is evaluated only after the formal parameters have been replaced by arguments.
  • The named formal parameters xi in Function[{x1,…},body] are treated as local, and are renamed xi$ when necessary to avoid confusion with actual arguments supplied to the function. »
  • Function constructs can be nested in any way. Each is treated as a scoping construct, with named inner variables being renamed if necessary. »
  • In Function[params, body, attrs], attrs can be a single attribute or a list of attributes. »
  • Function[Null,body,attrs] represents a function in which the parameters in body are given using # etc.

Examples

open allclose all

Basic Examples  (4)

Pure function with one parameter:

Pure function with two parameters:

Set to be a pure function:

Use the pure function:

Pick out named arguments from an association:

Scope  (15)

Use a Pure Function as an Argument  (5)

Map a pure function over a list:

Select with a pure function:

Use a pure function as a predicate:

Create an array from a pure function:

Sort by comparing the second part of each element:

Use a Pure Function as an Option Value  (3)

Specify a custom comparison function in FixedPoint:

Specify a custom color function:

Provide a custom distance function:

Return a Pure Function as a Result  (4)

Derivative of a pure function:

Derivative of Tan:

Solutions of differential equations may be expressed as pure functions:

Difference equations may return pure functions:

Function and Associations  (3)

#name is effectively a short form of #["name"]:

#name always refers to the association in the first argument:

Extract from an association slot other than the first:

Generalizations & Extensions  (4)

## stands for all arguments:

## n stands for arguments n and onward:

Create a pure function with attribute Listable:

#0 stands for the whole pure function:

A recursive definition for factorial using #0:

Applications  (3)

Turn a function that takes several arguments into one that takes a list of arguments:

A function that returns a function that multiplies its argument by n:

Preserve arguments in unevaluated form:

Properties & Relations  (11)

#1 uses only the first argument supplied; the rest are ignored:

Not using any arguments results in a constant pure function:

Replacements can be done inside pure functions:

Formal parameters are renamed whenever there is a possibility of confusion:

The names of the parameters do not matter:

However, reusing a name introduces a new scope:

Nested functions take their arguments one at a time:

f[#]& is the same as simply f in the univariate case:

In general, f[##]& is the same as f:

Turn a formula involving a variable into a pure function:

Use a formula in Table:

Use the corresponding pure function in an equivalent Array expression:

Special-purpose function constructs include InterpolatingFunction:

CompiledFunction:

NearestFunction:

LinearSolveFunction:

Possible Issues  (4)

& binds more loosely than ->, so it usually needs parentheses in rules:

& binds more loosely than ?, so it usually needs parentheses in pattern tests:

Function does not evaluate its body until the function is applied:

Supplying fewer than the required number of arguments generates an error:

Neat Examples  (2)

Define the recursion operator of recursion theory [more info]:

Use it to define the factorial function:

Newton's formula for finding a zero of a function:

Wolfram Research (1988), Function, Wolfram Language function, https://reference.wolfram.com/language/ref/Function.html (updated 2020).

Text

Wolfram Research (1988), Function, Wolfram Language function, https://reference.wolfram.com/language/ref/Function.html (updated 2020).

CMS

Wolfram Language. 1988. "Function." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Function.html.

APA

Wolfram Language. (1988). Function. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Function.html

BibTeX

@misc{reference.wolfram_2024_function, author="Wolfram Research", title="{Function}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Function.html}", note=[Accessed: 13-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_function, organization={Wolfram Research}, title={Function}, year={2020}, url={https://reference.wolfram.com/language/ref/Function.html}, note=[Accessed: 13-December-2024 ]}