GeometricTransformation
GeometricTransformation[g,tfun]
represents the result of applying the transformation function tfun to the geometric objects corresponding to the primitives g.
transforms geometric objects in g by effectively replacing every point r by m.r.
GeometricTransformation[g,{m,v}]
effectively replaces every point r by m.r+v.
GeometricTransformation[g,{t1,t2,…}]
represents multiple copies of g transformed by a collection of transformations.
Details and Options
- GeometricTransformation[g,…] remains unchanged under evaluation, but affects how g is rendered.
- GeometricTransformation works on lists of graphics primitives and directives in 2D and 3D.
- GeometricTransformation[g,{m,v}] effectively applies an affine transform to g.
- GeometricTransformation[g,{{mxx,myx},{mxy,myy}}] transforms the unit vectors
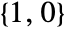and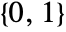 
to {mxx,mxy} and {myx,myy}, respectively. - For different spec, GeometricTransformation[g,{m,spec}] leaves fixed the following special points on the bounding box of g:
-
Center center Left midpoint of the left side Right midpoint of the right side Top midpoint of the top Bottom midpoint of the bottom Front midpoint of the front Back midpoint of the back {Left,Top}, etc. corners - For objects specified with scaled coordinates Scaled[{x,y}], GeometricTransformation effectively applies its transformation to the corresponding ordinary coordinates.
- Normal[expr] if possible replaces all GeometricTransformation[gi,…] constructs by versions of the gi in which the coordinates have explicitly been transformed.
- The following option can be given:
-
ContentSelectable Automatic whether to allow contents to be selected - For matrices m1 and m2, GeometricTransformation[GeometricTransformation[g,m1],m2] is equivalent to GeometricTransformation[g,m2.m1].
Examples
open allclose allBasic Examples (3)
Scope (5)
Properties & Relations (2)
Using {m,v} as the second argument is the same as using AffineTransform[{m,v}]:
When possible, Normal will perform the transformations explicitly:
Text
Wolfram Research (2007), GeometricTransformation, Wolfram Language function, https://reference.wolfram.com/language/ref/GeometricTransformation.html (updated 2010).
CMS
Wolfram Language. 2007. "GeometricTransformation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/GeometricTransformation.html.
APA
Wolfram Language. (2007). GeometricTransformation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricTransformation.html